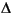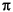mfilter
|
Construct a Bessel, Butterworth, Chebychev, or RC filter
|
nd2sys
|
Convert a SISO transfer function into a µ-Tools S matrix
|
pck
|
Create a S matrix from state-space data (A, B, C, D)
|
pss2sys
|
Convert an [A B;C D] matrix into a µ-Tools S matrix
|
sys2pss
|
Extract state-space matrix [A B; C D] from a S matrix
|
sysic
|
System interconnection program
|
unpck
|
Extract state-space data (A,B,C,D) from a S matrix
|
zp2sys
|
Convert transfer function poles and zeros to a S matrix
|
cf2sys
|
Create a S from a normalized coprime factorization
|
hankmr
|
Optimal Hankel norm approximation of a S matrix
|
sdecomp
|
Decompose a S matrix into two S matrices
|
sfrwtbal
|
Frequency weighted balanced realization of a S matrix
|
sfrwtbld
|
Stable frequency weighted realization of a S matrix
|
sncfbal
|
Balanced realization of coprime factors of a S matrix
|
srelbal
|
Stochastic balanced realization of a S matrix
|
sresid
|
Residualize states of a S matrix
|
strunc
|
Truncate states of a S matrix
|
sysbal
|
Balanced realization of a S matrix
|
dhfnorm
|
Calculate discrete-time  -norm of a stable S matrix -norm of a stable S matrix
|
dhfsyn
|
Discrete-time H control design control design
|
emargin
|
Normalized coprime factor robust stability margin
|
gap
|
Calculate the gap metric between S matrices
|
h2norm
|
Calculate 2-norm of a stable, strictly proper S matrix
|
h2syn
|
H2 control design
|
hinffi
|
H full information control design full information control design
|
hinfnorm
|
Calculate  -norm of a stable, proper S matrix -norm of a stable, proper S matrix
|
hinfsyn
|
H control design control design
|
hinfsyne
|
H minimum entropy control design minimum entropy control design
|
ncfsyn
|
H loopshaping control design loopshaping control design
|
nugap
|
Calculate the 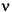 (nu) gap between S matrices (nu) gap between S matrices
|
pkvnorm
|
Peak norm of a V matrix
|
sdhfnorm
|
Sample-data  -norm of a stable S matrix -norm of a stable S matrix
|
sdhfsyn
|
Sample-data H control design control design
|
blknorm
|
Block norm of CV matrices
|
cmmusyn
|
Constant matrix µ synthesis
|
dkit
|
Automated D - K iteration for µ synthesis
|
dkitgui
|
Automated D - K iteration GUI for µ synthesis
|
dypert
|
Create a rational perturbation from frequency mu data
|
fitmag
|
Fit magnitude data with real, rational, transfer function
|
fitmaglp
|
Fit magnitude data with real, rational, transfer function
|
fitsys
|
Fit frequency response data with transfer function
|
genphase
|
Generate a minimum phase frequency response to magnitude data
|
genmu
|
Real and complex generalized µ-analysis of CV matrices
|
magfit
|
Fit magnitude data with real, rational, transfer function (a batch process)
|
mu
|
Real and complex µ-analysis of CV matrices
|
msf
|
Interactive D-scaling rational fit routine
|
muftbtch
|
Batch D-scaling rational fit routine
|
musynfit
|
Interactive D-scaling rational fit routine
|
musynflp
|
Interactive D-scaling rational fit routine (linear program)
|
muunwrap
|
Construct D-scaling and 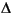 perturbation from perturbation from mu
|
randel
|
Generate a random perturbation
|
sisorat
|
Fit a frequency point with first order, all-pass, stable transfer function
|
unwrapd
|
Construct D-scaling from mu
|
unwrapp
|
Construct 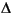 perturbation from perturbation from mu
|
wcperf
|
Worst-case performance for a given 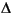
|
getiv
|
Get the independent variable of a V matrix
|
indvcmp
|
Compare the independent variable data of two V matrices
|
scliv
|
Scale the independent variable of a V matrix
|
sortiv
|
Sort the independent variable of a V matrix
|
tackon
|
String together V matrices
|
var2con
|
Convert a V matrix to a C matrix
|
varyrand
|
Generate a random V matrix
|
vfind
|
Find individual elements of a V matrix
|
vpck
|
Pack a V matrix
|
vunpck
|
Unpack a V matrix
|
xtract
|
Extract portions of a V matrix
|
xtracti
|
Extract portions of a V matrix using independent variable
|
vabs
|
Absolute value of a CV matrix
|
vceil
|
Round elements of CV matrices towards 
|
vdet
|
Determinant of CV matrices
|
vdiag
|
Diagonal of CV matrices
|
veig
|
Eigenvalue decomposition of CV matrices
|
vexpm
|
Exponential of CV matrices
|
vfft
|
FFT for V matrices
|
vfloor
|
Round elements of CV matrices towards -
|
vifft
|
Inverse FFT for V matrices
|
vimag
|
Imaginary part of a CV matrix
|
vinv
|
Inverse of a CV matrix
|
vnorm
|
Norm of CV matrices
|
vpinv
|
Pseudoinverse of a CV matrix
|
vpoly
|
Characteristic polynomial of CV matrices
|
vrcond
|
Condition number of a CV matrix
|
vreal
|
Real part of a CV matrix
|
vroots
|
Polynomial roots of CV matrices
|
vschur
|
Schur form of a CV matrix
|
vspect
|
Signal processing spectrum command for V matrices
|
vsvd
|
Singular value decomposition of a CV matrix
|




 Analysis and Synthesis Functions
Analysis and Synthesis Functions -norm of a stable S matrix
-norm of a stable S matrix control design
control design full information control design
full information control design -norm of a stable, proper S matrix
-norm of a stable, proper S matrix control design
control design minimum entropy control design
minimum entropy control design loopshaping control design
loopshaping control design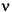 (nu) gap between S matrices
(nu) gap between S matrices -norm of a stable S matrix
-norm of a stable S matrix control design
control design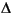 perturbation from
perturbation from  perturbation from
perturbation from