Mu Analysis and Synthesis Toolbox

Fit single-input/single-output magnitude data with a real, rational, minimum phase transfer function

Syntax

• sys = fitmag(magdata,weight,heading,oldfit,...
                         dmdi,upbd,blk,blknum) 
  resp = genphase(d) 
  sys = fitmaglp(magdata,weight,heading,oldfit,...
                         dmdi,upbd,blk,blknum) 
  [sys,fit] = magfit(magdata,dim,weight)
  

Description
fitmag fits a stable, minimum phase transfer function to magnitude data, magdata, with a supplied frequency domain weighting function, weight. Both of these are VARYING matrices, with identical independent variable values. fitmag uses genphase to generate phase data, and fitsys to do the fit.

genphase uses the complex-cepstrum algorithm to generate a complex frequency response, resp, whose magnitude is equal to the real, positive response d, but whose phase corresponds to a stable, minimum phase function.

fitmaglp has the same inputs, outputs, and user interaction as fitmag , but uses a linear programming approach to do the fitting instead of fitsys and genphase.

fitmag and fitmaglp have the additional input arguments dmdi, upbd, blk, and blknum. These arguments are used exclusively with D-K iteration when called by musynfit and musynflp. In this case, the magdata is the dvec output of the mu program and corresponds to the blknum'th frequency varying D scale to be fit. weight corresponds to a measure of the sensitivity of mu to changes in the D scales at each frequency. This is the sens output from mu. heading is a string variable denoting the title of the plot and oldfit is usually the D scalings from the previous D-K iteration.

dmdi represents the VARYING matrix analyzed using mu. upbd is the upper bound calculated using mu of dmdi with the perturbation block structure blk. The last argument, blknum, corresponds to the current D scale in the block structure being fit with fitmag or fitmaglp. Upon fitting the magnitude data, magdata, the resulting transfer function sys is absorbed into the original matrix dmdi and plotted along with the mu upper bound on the lower graph.

magfit is a batch version of fitmaglp that eliminates the user interaction. The weight is optional, but dim is a required argument of parameters for the linear program. dim has the form [hmax htol nmin nmax] where

• hmax is a measure of the allowable error in the fit.
• htol is a measure of the accuracy with which the optimization is carried out.
• nmin and nmax are the minimum and maximum orders considered for the curve fit.

Examples
Create a second-order transfer function sys to test fitmag. Fit its magnitude data with a first- and second-order transfer function via fitmag.

• sys = nd2sys([1 -5 12],[1 2 7]); 
  w = logspace(-2,2,200); 
  sysg = frsp(sys,w); 
  wgt = 0.2; 
  wgtg = frsp(wgt,w); 
  sysfit = fitmag(vabs(sysg),wgtg); 
  ENTER ORDER OF CURVE FIT or 'drawmag' 1
  

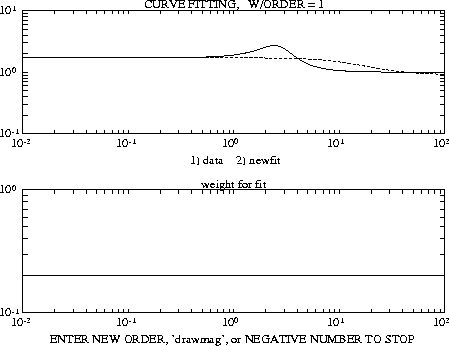
A first-order fit does not accurately respresent the frequency data as shown in the above figure. The solid line represents the curve fit and the dashed line represents the original frequency data. You can try and fit the data again with a second-order system.

• ENTER ORDER, 'drawmag', or NEGATIVE TO STOP 2
  
  
  
  ENTER ORDER, 'drawmag', or NEGATIVE TO STOP -1
  

Algorithm
The algorithm for fitmag is as follows. On a log-log scale, the magnitude data is interpolated linearly, with a very fine discretization. Then, using the complex cepstrum algorithm, the phase, associated with a stable, minimum phase, real, rational transfer function with the same magnitude as the magdata variable is generated. This involves two fft's, and logarithmic/exponential conversions. With the new phase data, and the input magnitude data, the MATLAB function invfreqs is used to find a real, rational transfer function that fits the data. heading is an optional title and oldfit is an optional previous fit that can be added to the graphs if they are included. These options are used in the program musynfit.

The algorithm for magfit is as follows. The system sys is derived by solving a linear program and searching over a parameter h according to the following specification. Let m be the given magnitude data, g the transfer function of sys and w the values of weight; then h is found such that at each frequency,

where

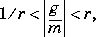
The order of sys is increased until an h less than hmax is obtained or nmax is reached. The minimum value of h at this order is then determined to an accuracy of htol.

Problems
For problems with very coarse data, fitmag may give incorrect answers, even if the data was generated by taking the frequency response of a linear system. The inaccuracy arises in the log-log interpolation step, which is used in the phase calculation. This step is avoided in magfit. Hence, for coarse data sets, magfit should be used. fitmaglp and magfit appear to be sometimes slower than fitmag.

Reference
Oppenheim, A.V., and R.W. Schaffer, Digital Signal Processing, Prentice Hall, New Jersey, 1975, pp. 513.

See Also
fitsys, invfreqs, musynfit, musynflp, muftbtch

dypert, sisorat

fitsys