| Mu Analysis and Synthesis Toolbox | |
srelbal calculates the stochastically balanced realization of a SYSTEM matrix, sfrwtbal, the frequency weighted balanced realization for performing relative error, and sfrwtbld, the frequency weighted model order reduction. sncfbal calculates the normalized coprime factorizations. sdecomp decomposes a SYSTEM matrix as the sum of stable and unstable systems.
Syntax
[sysb,relsv,sysfact] = srelbal(sys,tol) [sys1,sig1] = sfrwtbal(sys,wt1,wt2) syshat = sfrwtbld(sys1hat,wt1,wt2) [sysnlcf,signcf,sysnrcf] = sncfbal(sys,tol) [sysst,sysun] = sdecomp(sys,bord,fl)
Description
srelbal performs a stochastically balanced realization of the input SYSTEM matrix. sys must be stable and be of full column rank at infinite frequency, but not necessarily square or minimum phase. Difficulties may occur if sys has zeros on the imaginary axis. sysb will have the same transfer function as sys, and sysfact gives the stable minimum phase system such that sys~ sys = sysfact sysfact~. Note that sys~ denotes cjt(sys). If [a,b,c,d] = unpck(sysb) and [af,bf,cf,df] = unpck(sysfact), then the realization [a,bf,c,0] will be balanced with Hankel singular values relsv, and will also equal the stable part of sys*sysfact~-1. A reduced-order system can be obtained by strunc(sysb,k) that will have guaranteed performance in the relative error.
sfrwtbal performs a frequency-weighted balancing. It calculates the stable part of (wt1) ~-1 * sys* (wt2)~-1 and sys1 is a balanced realization of this, with Hankel singular values sig1. wt1 and wt2 must be stable and minimum phase, square and of compatible dimensions with sys. wt2 has the identity as default value. sys must be stable. The resulting system sys1 can then be approximated by sys1hat of order k using, for example, hankmr, and an approximation syshat to sys is obtained by sfrwtbld, which calculates the stable part of (wt1)~ *sys1hat*(wt2)~ using sdecomp.
A general lower bound on the frequency weighted approximation error is given by
(wt1) ~-1(sys - syshat)(wt2)~-1||·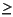 
sig1(k + 1)
where in the relative error case wt1 is the identity and wt2 = sysfact.
sncfbal produces balanced realizations of the normalized left and right coprime factorizations of a SYSTEM matrix. That is for a transfer function G, balanced state-space realizations are calculated for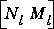 
and 
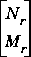, where 
, 
, 
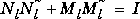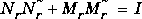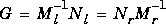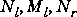, and 
, and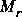 
are all stable. The Hankel singular values of both 
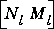and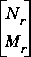 
are given by the column vector signcf. Model reduction for these systems can then be performed using strunc or hankmr. The method is well suited to plant or controller reduction in feedback systems.
sdecomp decomposes a system into the sum of two systems, sys = madd(sysst,sysun). sysst has the real parts of all its poles < bord and sysun has the real parts of all its poles 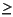bord. bord has default value 0. The D matrix for sysun is zero unless fl = 'd' when that for sysst is zero.
srelbal, sfrwtbal , sfrwtbld, sncfbal, and sdecomp are restricted to be used on continuous-time SYSTEM matrices.
Examples
Given the system
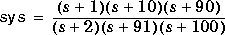
reduce the system to two and one states, respectively. An approximate system of order 1 or 2 can be obtained as follows.
sys = zp2sys([-1 -10 -90],[-2 -91 -100]); [sysb,relsv,sysfact] = srelbal(sys); disp(relsv') 8.5985e-012.0777e-012.1769e-04 sysrel1 = strunc(sysb,1); sysrel2 = strunc(sysb,2);
The reduced-order models of order k can be obtained in the frequency weighted case as follows:
wt1 = nd2sys([1 10],[1 1]); [sys1,sig1] = sfrwtbal(sys,wt1); disp(sig1'); 4.1873e-014.6472e-031.0280e-04 sys1hat = hankmr(sys1,sig1,1,'d'); syshat = sfrwtbld(sys1hat,wt1); disp(hinfnorm(mmult(msub(sys,syshat),minv(wt1)))); 4.6471e-034.6517e-03Inf
Now consider approximating the unstable third order system,
using sncfbal. First the balanced realization of the normalized left coprime factors is calculated, then this is truncated to two states and the reduced-order system recovered from these normalized coprime factors using starp.
sys = zp2sys([],[0 1 -10],10); [sysnlcf,signcf] = sncfbal(sys); disp(signcf') 9.6700e-015.2382e-012.3538e-02 sysnlcfr = strunc(sysnlcf,2); sysr = starp(mmult([1;1],msub(sysnlcfr,[0 1])),-1,1,1)
signcf(1) can be used to predict the possible robust stability to perturbations in the coprime factors, and the potential for model-order reduction of the controller is given by signcf(2:3), McFarlane and Glover (1989). In this example the maximum stablizable perturbations in the coprime factors is given by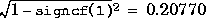 
. Furthermore if a controller is designed to be optimal for the second-order reduced model, then its stability margin will be at least
Algorithm
The algorithms are based on the results in the following papers.
Reference
Anderson, B.D.O., and Y. Liu, "Controller reduction: Concepts and Approaches," IEEE Transactions on Automatic Control, vol. AC-34, pp. 802-812, 1989.
Desai, U.B., and D. Pal, "A transformation approach to stochastic model reduction," IEEE Transactions on Automatic Control, vol. AC-29, pp. 1097-1100, 1984.
Glover, K., "Multiplicative approximation of linear multivariable systems with error bounds," Proceedings of the American Control Conference, Seattle, pp. 1705-1709, 1986.
Latham, G.A., and B.D.O. Anderson, "Frequency-weighted optimal Hankel norm approximation of state transfer functions," Systems and Control Letters, vol. 5, pp. 229-236, 1985.
McFarlane, D.C., and K. Glover, Robust Controller Design using Normalised Coprime Factor Plant Descriptions, Springer-Verlag, Lecture Notes in Control and Information Sciences, vol. 138, 1989.
Wang, W., and M.G. Safonov, "A tighter relative error bound for balanced stochastic truncation," Systems and Control Letters, vol. 14, pp. 307-317, 1990.
See Also
hankmr, sysbal, sresid, strunc
| spoles | sresid, strunc | |