

| Mu Analysis and Synthesis Toolbox |   |
Calculate the complex frequency response of a linear system
Syntax
Description
frsp calculates the complex frequency response of a given SYSTEM matrix (sys) for a vector of frequency points (omega). The output matrix out is a frequency dependent VARYING matrix containing the frequency response of the input system sys at the frequency values contained in the vector omega . For systems with multiple inputs and outputs, a multivariable frequency response is returned.
|
VARYING frequency response matrix |
The vector of frequency points is assumed to be real and can be generated from the MATLAB command logspace or linspace. Given a continuous system sys, of the form
and an input vector, omega , with N frequencies, [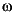 1,
1, 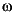 2,. . .,
2,. . .,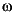 N],
N], frsp evaluates the following equation
C(j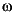 iI - A)-1B + D,
iI - A)-1B + D, i = 1,. . .,N
You can specify a discrete time evaluation by specifying an optional sampling time, T. For the discrete time case each matrix in the VARYING output is given by
Note that setting T = 0 implies that a continuous frequency response is to be performed and not to evaluate
Examples
The SYSTEM matrix sys is constructed to have two inputs and two outputs with poles at -2 and -10. A frequency vector omega is constructed with 30 points log spaced between .1 and 100 rad/s. The complex frequency response of sys is calculated and its values between 3.5 and 4.6 rad/s are displayed.
a = [-2 0;0 -10];b = [.2 .12; -.3 .4];c = [.3 .7; 2 -1];
sys = pck(a,b,c);
omega = logspace(-1,2,30);
sysg = frsp(sys,omega);
see(xtract(sysg,3.5,4.6))
2 rows 2 columns
iv = 3.56225
-0.0114 - 0.0062i 0.0292 - 0.0165i
0.0746 - 0.0949i -0.0067 - 0.0386i
iv = 4.52035
-0.0125 - 0.0032i 0.0262 - 0.0172i
0.0577 - 0.0853i -0.0136 - 0.0294i
frsp with the default variables set. A plot of the frequency response is shown with the four line types corresponding to the sysg(1,1), sysg(1,2), sysg(2,1), and the sysg(2,2) elements.
To demonstrate the calculation of a discrete frequency response, convert this system into a digital system via the bilinear transformation. The sample frequency is chosen as 100 radians/second.
T = 2*pi/100;
dsys = tustin(sys,T);
omega = sort([omega,logspace(0,2,60)]);
dsysg = frsp(dsys,,T);
vplot('bode',sysg);
title('Complex frequency response example - discrete time')
 by specifying T = 1. A Chebyshev type II filter is designed and its magnitude is plotted to demonstrate this feature.
by specifying T = 1. A Chebyshev type II filter is designed and its magnitude is plotted to demonstrate this feature.
[a,b,c,d] = cheby2(11,30,0.3);
dfilt = pck(a,b,c,d);
omega = [0:pi/100:pi*99/100];
dsysg = frsp(dfilt, omega,1);
vplot('iv,lm',dsysg);
xlabel('frequency on unit circle')
ylabel('Magnitude')
title('Complex frequency response on the unit circle')
Algorithm
The algorithm to calculate the complex frequency response involves an matrix inverse problem, which is solved via a Hessenberg matrix. If balflg is set to 0, the frequency response balances the SYSTEM A matrix (using the MATLAB balance command) prior to calculation of the Hessenberg form.
Note:
Balancing the system may cause errors in the frequency response. If the output of frsp is questioned, compare the results with balancing and without balancing the SYSTEM prior to calculating the frequency response.
Reference
Laub, A.J., "Efficient Multivariable Frequency Response Computations," IEEE Transactions on Automatic Control, vol. AC-26, No. 2, pp. 407-408, April, 1981.
See Also
balance, hess, samhld, tustin, vplot
 | fitsys | gap, nugap |  |