hinfsyn (Mu Analysis and Synthesis Toolbox)

Mu Analysis and Synthesis Toolbox

hinfsyn

Compute an H controller for a SYSTEM interconnection matrix

Syntax

[k,g,gfin,ax,ay,hamx,hamy] = 
                       hinfsyn(p,nmeas,ncon,gmin,gmax,tol,ricmethd,epr,epp)

Description
hinfsyn calculates an H controller, which achieves the infinity norm gfin for the interconnection structure p. The controller, k, stabilizes the SYSTEM matrix p and has the same number of states as p. The SYSTEM p is partitioned

where B₁are the disturbance inputs, B₂ are the control inputs, C₁ are the errors to be kept small, and C₂ are the output measurements provided to the controller. B₂ has column size (ncon) and C₂ has row size (nmeas).

The closed-loop system is returned in g. The program provides a 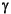iteration using the bisection method. Given a high and low value of 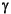, gmax and gmin, the bisection method is used to iterate on the value of 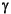in an effort to approach the optimal H control design. If the value of gmax is equal to gmin, only one 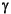value is tested. The stopping criteria for the bisection algorithm requires the relative difference between the last 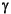value that failed and the last 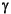value that passed be less than tol. You can select either the eigenvalue or Schur method the Riccati equations. The eigenvalue method is faster but can have numerical problems, while the Schur method is slower but generally more reliable.

The algorithm employed requires tests to determine whether a solution exists for a given 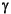value. epr is used as a measure of when the Hamiltonian matrix has imaginary eigenvalues and epp is used to determine whether the Riccati solutions are positive semi-definite. The conditions checked for the existence of a solution are:

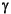H and J Hamiltionian matrices (which are formed from the state-space data of P and the level) must have no imaginary-axis eigenvalues.
the stabilizing Ricatti solutions X and Y associated with the Hamiltionian matrices must exist and be positive, semi-definite.
spectral radius of (X,Y) must be less than or equal to 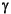².

The selection of epr and epp should be based on your knowledge of the numerical conditioning of the interconnection structure p. The following assumptions are made in the implementation of the hinfsyn algorithm and must be satisfied:

(i) (A,B₂) is stabilizable and (C₂,A) detectable.

(ii) D₁₂ and D₂₁ have full rank.

(iii)

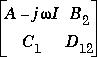
has full column rank for all R.

(iv)

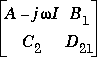
has full row rank for all 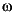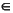R.

Inputs arguments:

p
SYSTEM interconnection structure matrix

nmeas
number of measurements output to controller

ncon
number of control inputs

gmin
lower bound on

gmax
upper bound on

tol
relative difference between final values

ricmethod
1 Eigenvalue decomposition with balancing
2 Schur decomposition with balancing (default)
-2 Schur decomposition with no balancing

epr
measure of when a real part of an eigenvalue of the Hamiltonian matrix is zero (default epr = 1e-10)

epp
positive definite determination of the X and Y solution (default epp = 1e-6)

`p`	SYSTEM interconnection structure matrix
`nmeas`	number of measurements output to controller
`ncon`	number of control inputs
`gmin`	lower bound on
`gmax`	upper bound on
`tol`	relative difference between final values
`ricmethod`	1 Eigenvalue decomposition with balancing 2 Schur decomposition with balancing (default) -2 Schur decomposition with no balancing
`epr`	measure of when a real part of an eigenvalue of the Hamiltonian matrix is zero (default `epr` = 1e-10)
`epp`	positive definite determination of the X and Y solution (default `epp` = 1e-6)

Output arguments:

k
H (sub) optimal controller

g
closed-loop system with H controller

gfin
final achieved

ax
X Riccati solution as a VARYING matrix with independent variable

ay
Y Riccati solution as a VARYING matrix with independent variable

hamx
H Hamiltonian matrix as a VARYING matrix with independent variable

hamy
J Hamiltonian matrix as a VARYING matrix with independent variable

`k`	H (sub) optimal controller
`g`	closed-loop system with H controller
`gfin`	final achieved
`ax`	X Riccati solution as a VARYING matrix with independent variable
`ay`	Y Riccati solution as a VARYING matrix with independent variable
`hamx`	H Hamiltonian matrix as a VARYING matrix with independent variable
`hamy`	J Hamiltonian matrix as a VARYING matrix with independent variable

Note that the outputs ax, ay, hamx, and hamy correspond to scaled or balanced data.

The hinfsyn program displays several variables, which can be checked to ensure that the above conditions are being satisfied. For each 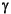value being tested, the minimum magnitude, real part of the eigenvalues of the X and Y Hamiltonian matrices are displayed along with the minimum eigenvalue of X and Y, which are the solutions to the X and Y Riccati equations, respectively. The maximum eigenvalue of XY, scaled by 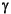^-2,is also displayed. A # sign is placed to the right of the condition that failed in the printout.

Note:
When a Hamiltonian has repeated eigenvalues, solving the Riccati equation via the eigenvalue method (ric_eig) may have problems. This is due to the MATLAB command eig incorrectly selecting the eigenvectors associated with the repeated roots.

Examples
This example is taken from the "HIMAT Robust Performance Design Example" section in Chapter 7. himat_ic contains the open-loop interconnection structure. Design an H (sub)optimal controller for the SYSTEM matrix, himat_ic, with two sensor measurements, two error signals, two actuator inputs, two disturbances, and eight states. The range of 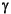is selected to be between 1.0 and 10.0 with a tolerance, tol, on the relative closeness of the final 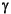solution of 0.1. The Schur decompostion method, ric_schr, is used for solution of the Riccati equations. The program outputs at each iteration the current 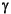value being tested, and eigenvalue information about the H and J Hamiltonian matrices and X and Y Riccati solutions. At the end of each iteration a (p) denoting the tested 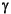value passed or an (f) denoting a failure is displayed. Upon finishing, hinfsyn prints out the 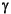value achieved.

nmeas = 2;% number of sensor measurements 
ncont = 2;% number of control inputs 
gmin = 1;% minimum gamma value to be tested 
gmax = 10;% maximum gamma value to be tested 
tol = .1;% tolerance on the gamma stopping value 
ric = 2;% Riccati equation solved via the Schur method 
minfo(himat_ic)% SYSTEM interconnection structure
system: 8 states6 outputs6 inputs

[k,g] = hinfsyn(himat_ic,nmeas,ncon,gmin,gmax,tol,ric);
Test bounds: 1.0000 < gamma <=10.0000

gamma   hamx_eig   xinf_eig  hamy_eig  yinf_eig  nrho_xy  p/f
10.000  2.3e-02    2.1e-10   2.3e-02  -3.7e-11   0.022     p
5.500   2.3e-02    2.1e-10   2.3e-02  -0.0e+00   0.075     p
3.250   2.3e-02    2.2e-10   2.3e-02  -0.0e+00   0.222     p
2.125   2.3e-02    2.2e-10   2.3e-02  -0.0e+00   0.564     p
1.562   2.3e-02    2.4e-10   2.3e-02  -0.0e+00   1.198#    f
1.844   2.3e-02    2.3e-10   2.3e-02  -0.0e+00   0.789     p
1.703   2.3e-02    2.3e-10   2.3e-02  -2.1e-11   0.959     p
1.633   2.3e-02    2.3e-10   2.3e-02  -0.0e+00   1.068#    f

Gamma value achieved:1.7031

Algorithm
hinfsyn uses the formulae described in the Glover and Doyle, 1988, paper for solution to the optimal H control design problem. There are a number of research issues that need to be addressed for the "best" solution of the Riccati equations but only two of the standard methods are included.

Subroutines called. hinf_st, hinf_sp, hinf_c, and

hinf_gam
hinf_gam

calls: ric_eig, ric_schr, csord, cgivens

Reference
Doyle, J.C., K. Glover, P. Khargonekar, and B. Francis, "State-space solutions to standard H₂ and H control problems," IEEE Transactions on Automatic Control, vol. 34, no. 8, pp. 831-847, August 1989.

Glover, K., and J.C. Doyle, "State-space formulae for all stabilizing controllers that satisfy an Hnorm bound and relations to risk sensitivity," Systems and Control Letters, vol. 11, pp. 167-172, 1988.

See Also
hinffi, hinfnorm, hinfsyne, h2syn, h2norm, ric_eig, ric_schr

hinffi hinfsyne