Mu Analysis and Synthesis Toolbox

Create a matrix which is made up of norms of subblocks. Used in conjunction with mu (µ)

Syntax

• matout = blknorm(matin,blk)
  

Description
blknorm computes the maximum singular value of the subblocks of matin, using the information in the perturbation block structure, blk. The output of blknorm is matout whose entries are the maximum singular value of the subblocks of matin with these norms as elements. This helps to show which parts of the matrix are contributing to making µ large. A more complete description of the perturbation block structure, blk, can be found with the command mu and in Chapter 4. blknorm is best used on scaled matrices from the upper bound for µ. Repeated 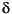I blocks are treated the same way as full blocks. The function blknorm can be applied to both CONSTANT and VARYING matrices.

Examples
Create a 4 x 3 random matrix and determine its subblock norms for two different block structures. The first block structure consists of a two element repeated block and a 1 x 2 full block. The second block structure consists of a 1 x 1 block, a 1 x 2 full block, and a 1 x 1 block.

• m = crand(4,3);
  disp(m)
  
  0.7012 + 0.9826i    0.0475 + 0.0727i    0.7564 + 0.4364i
  0.9103 + 0.7227i    0.7361 + 0.6316i    0.9910 + 0.7665i
  0.7622 + 0.7534i    0.3282 + 0.8847i    0.3653 + 0.4777i
  0.2625 + 0.6515i    0.6326 + 0.2727i    0.2470 + 0.2378i
  
  disp(blknorm(m,[2 0; 1 2]))
      1.8498    1.5272
      1.6656    0.6923
  
  mprintf(blknorm(m,[1 1; 1 2; 1 1]), '%6.2f')
      1.21    0.09    0.87
      1.58    1.35    1.39
      0.70    0.69    0.34
  

Algorithm
The maximum singular value of each block associated with the blk structure is calculated via the MATLAB norm.

See Also
mu, norm, vnorm

abv, daug, sbs

cjt, transp, vcjt, vtp