cmmusyn (Mu Analysis and Synthesis Toolbox)

Mu Analysis and Synthesis Toolbox

cmmusyn

Approximately solves the constant-matrix µ-synthesis problem, via the minimization

for given matrices R 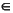Cnxm, U 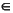Cnxr,V 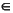Ctxm, and a set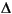 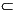Cmxn.

Syntax

[bnd,dvec,gvec,qopt] = cmmusyn(R,U,V,blk);

Algorithm
This works for CONSTANT or VARYING data in R, U, and V. If two or more matrices are VARYING, the independent variable values of these matrices must be the same.

The approximation to solving the constant matrix µ synthesis problem is two-fold: only the upper bound for µ is minimized, and the minimzation is not convex, hence the optimum is generally not found. If U is full column rank, or V is full row rank, then the problem can (and is) cast as a convex problem, [PacZPB], and the global optimizer (for the upper bound for µ) is calculated.

The upper bound is returned in bnd, and the optimizing Q is returned in qopt. The scaling matrices associated with the upper bound are in dvec and gvec and may be unwrapped into block diagonal form using muunwrap.

Reference
PacZPB: A. K. Packard, K. Zhou, P. Pandey, and G. Becker, "A collection of robust control problems leading to LMI's," 30th IEEE Conference on Decision and Control, pp. 1245-1250, Brighton, UK, 1991.

See Also
genmu, mu

cjt, transp, vcjt, vtp cos_tr, sin_tr, step_tr