| Mu Analysis and Synthesis Toolbox | |
Solution of a Riccati equation via eigenvalue decomposition
Syntax
Description
ric_eig (along with a call to x=x2/x1) solves the Riccati equation,
with the constraint that the matrix A + RX has all of its eigenvalues in open left-half plane. The data matrices A, R and Q come from the input Hamiltonian matrix, ham, in the form
and it is assumed that R = R', Q = Q'.
If ham has no j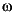
axis eigenvalues, then there exists n x n matrices x1 and x2 such that [x1; x2] spans the n-dimensional stable, invariant subspace of ham. If the matrix x1 is indeed invertible, then X := x2 * x1-1 satisfies the Riccati equation and results in A + RX being stable. It is the only such matrix with these properties.
ric_eig has internal error checking and returns a fail value of 1 if j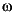 axis eigenvalues of ham are found. If this occurs, there is no n-dimensional, stable invariant subspace, and hence no stabilizing Riccati solution. An eigenvalue is considered to be purely imaginary if the magnitude of the real part is less than epp. The minimum real part of the eigenvalues is returned in reig_min. epp is an optional argument and its default value is 1e - 10.
Note:
When a Hamiltonian has repeated eigenvalues, solving the Riccati equation via the eigenvalue method may have problems. This is due to the MATLAB command eig incorrectly selecting the eigenvectors associated with the repeated roots.
Algorithm
Under the assumption that the Hamiltonian matrix has a full set of eigenvectors, the stable-invariant subspace is spanned by the eigenvectors associated with the stable eigenvalues. Hence, an eigenvalue-eigenvector decomposition can obtain the stable invariant subspace of the Hamiltonian matrix, ham. Assuming there are no j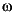 axis eigenvalues, and that there is a full set of eigenvectors, the two components, x1 and x2, can be generated by choosing the eigenvectors associated with the stable eigenvalues. The ric_eig subroutine operates on the assumption that the Jordan form of the Hamiltonian is diagonal, and returns the stable invariant subspace, as spanned by the eigenvectors, in the two block form described above.
See Also
eig, h2syn, hinfsyn, hinffi, ric_schr
| pkvnorm, vnorm | ric_schr | |
