starp (Mu Analysis and Synthesis Toolbox)

Mu Analysis and Synthesis Toolbox

starp

Form the Redheffer star product of two VARYING/SYSTEM/CONSTANT matrices. The star product is a generalization of a linear fractional transformation

Syntax

```
sysout = starp(top,bot,dim1,dim2)
```

Description
Connects the two matrices top and bot in the star product loop shown below.

The last dim1 outputs of top are fed to the first dim1 inputs of bot, and the first dim2 outputs of bot are fed into the last dim2 inputs of top. The remaining inputs and outputs constitute sysout. By this description, the dimensions must satisfy

min(dim_out(top),dim_in(bot)) 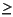dim1

min(dim_out(bot),dim_in(top)) 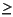dim2

Further restrictions also arise

IF
dim1 = dim_out(top) & dim2 = dim_out(bot)

THEN
there are no outputs remaining in the interconnection

IF
dim1 = dim_in(bot) & dim2 = dim_in(top)

THEN
there are no inputs remaining in the interconnection

`IF`	`dim1 = dim_out(top)` & `dim2 = dim_out(bot)`
`THEN`	there are no outputs remaining in the interconnection
`IF`	`dim1 = dim_in(bot)` & `dim2 = dim_in(top)`
`THEN`	there are no inputs remaining in the interconnection

In either case, it is unclear what to return as sysout, so it is returned empty. There is one exception to this situation. If either top or bot is a SYSTEM matrix with a nonzero number of states, and all of the equalities in the both of the above IF conditions hold (hence there are no inputs or outputs in the interconnection), then sysout will be a CONSTANT matrix, and will be the A matrix governing the internal dynamics of the loop.

As usual, the only types of matrices that cannot be combined are SYSTEM matrices with VARYING matrices.

If only two arguments are given (i.e., no dimensions specified),

```
out = starp(top,bot);
```

then the operation is equivalent to

dim1 = min(ynum(top),unum(bot)); 
dim2 = min(unum(top),ynum(bot)); 
out = starp(top,bot,dim1,dim2);

Algorithm
The "m-Tools Commands for LFTs" section in Chapter 4 provides details of the star product formulae.

Reference
Redheffer, R., "Inequalities for a matrix Riccati equation," Journal of Mathematics and Mechanics, vol. 8, no. 3, 1959.

See Also
sysic

sresid, strunc statecc, strans