Mu Analysis and Synthesis Toolbox

Compute an ordered, complex Schur form matrix

Syntax

• [v,t,flgout,reig_min] = csord(m,epp,flgord,flgjw,flgeig)
  

Description
The csord function produces an ordered, complex Schur form matrix of the input CONSTANT square matrix m with

The MATLAB function schur is called, which results in an unordered Schur form matrix. The subroutine cgivens forms a complex Givens rotation matrix, which orders the t matrix as you define it. The v matrix is the transformation matrix. A series of optional input flags can be set:

epp	user-supplied zero tolerance (default epp = 0)
flgord=0 flgord=1	order eigenvalues in ascending real part (default) partial real part ordering, with real parts less than zero first, then the j axis eigenvalues and finally the real parts greater than zero
flgjw=0 flgjw=1	no exit condition on eigenvalue location (default) exit if abs(real(eigenvalues(i)))< epp
flgeig=0 flgeig=1	no exit condition on half-plane eigenvalue distribution (default) exit if length(real(eigenvalues)>0) = length(real(eigenvalues)<0)

The output flag flgout is nominally 0. flout is set to 1 if there are j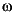-axis eigenvalues, set to 2 if there are an unequal number of positive and negative eigenvalues, or set to 3 if both conditions occur. The fourth output argument, reig_min, is the minimum, magnitude real part of the eigenvalues of m.

The ric_schr routine calls csord to solve for a stabilizing solution to a matrix Riccati equation. In this case, the m matrix has a special structure, and failure modes are flagged to avoid extra, unnecessary computations.

Algorithm
The eigenvalues are reordered by iterating through each of them and interchanging them via a bubble sort based on the input flag, flgord. The subroutine cgivens exchanges the out of order eigenvalues.

Reference
Golub, G.H. and C.F. Van Loan, Matrix Computations, The Johns Hopkins University Press, 1983.

See Also
cgivens, ric_schr, rsf2csf, schur

crand, crandn, sysrand, varyrand

dhfnorm