Mu Analysis and Synthesis Toolbox

Calculate the H₂, H norms of a SYSTEM matrix

Syntax

• out = h2norm(sys) 
  out = hinfnorm(sys,tol)
  

Description
h2norm calculates the 2-norm of a stable, strictly proper SYSTEM matrix. The output is a scalar, whose value is the 2-norm of the system.

The output from hinfnorm is a 1 x 3 vector, out, which is made up (in order) of a lower bound for ||sys||_·, an upper bound for ||sys||_·, and a frequency, 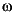o, at which the lower bound is achieved.

The ||·||_· norm calculation is an iterative process and requires a test to stop. The variable tol specifies the tolerance used to calculate the ||sys||_·. The iteration stops when

(the current upper bound) 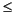(1 + tol) x (the current lower bound).

The default value of tol is 0.001.

Algorithm
The H₂ norm of a SYSTEM follows from the solution to the Lyapunov equation.

AX + XA' + BB' = 0,

with ||sys||₂ = trace (CXC').

Calculation of the H norm requires checking for j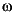 axis eigenvalues of a Hamiltonian matrix, H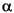, which depends on a parameter 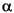. If H 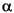has no j 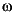axis eigenvalues, then the ||·||_· norm of the SYSTEM matrix is less than 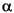. If the matrix H 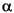does have j 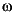axis eigenvalues, then these occur at the frequencies where the transfer matrix has a singular value (not necessarily the maximum) equal to 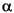. By iterating, the value of the ||·||_· norm can be obtained.

Reference
Boyd, S., K. Balakrishnan and P. Kabamba, "A bisection method for computing the H norm of a transfer matrix and related problems," Math Control Signals and Systems, 2(3), pp. 207-219, 1989.

Boyd, S., and K. Balakrishnan, "A regularity result for the singular values of a transfer matrix and a quadratically convergent algorithm for computing its H norm," Systems and Control Letters, vol. 15-1, 1990.

Bruinsma, O., and M. Steinbuch, "A fast algorithm to compute theH norm of a transfer function matrix," Systems and Control Letters, vol. 14, pp. 287-293, 1990.

See Also
hinfsyn, h2syn, ric_eig, ric_schr

getiv, sortiv, tackon

h2syn