dkit (Mu Analysis and Synthesis Toolbox)

Mu Analysis and Synthesis Toolbox

dkit

A script file for µ synthesis via D-K iteration

Syntax

```
dkit
```

Description
dkit is a µ-Tools script file for D-K iteration. The D-K iteration procedure is an approximation to µ synthesis control design. It involves a sequence of minimizations, first over the controller variable K (holding the D variable associated with the scaled µ upper bound fixed), and then over the D variable (holding the controller K variable fixed). The D-K iteration procedure is not guaranteed to converge to the minimum µ value, but often works well in practice. A detailed description of the D-K iteration can be found in Chapter 5.

dkit automates the D-K iteration procedure but requires the initialization of several variables. The file dk_defin.m is an example of the information required by dkit. You can copy this file from the µ-Tools subroutine directory mutools/subs and modify it for your application. This file can also be renamed. After renaming, assign the variable DK_DEF_NAME in the MATLAB workspace to the (character string) name of the new file containing the user-defined variables for dkit. For example, if the filename containing the setup data is himat_def.m, then

```
DK_DEF_NAME = 'himat_def';
```

should be executed in the MATLAB workspace.

The following is a list of what occurs during a single, complete step of the D-K iteration.

1.: Upon running dkit, the program prompts you for starting D-K iteration number.

```
Starting mu iteration #:
```

: Type 1 to indicate the first D-K iteration.

2.: (In the 1st iteration, this step is skipped.) The µ calculation (from the previous step) provides a frequency-dependent scaling matrices, D_f. The fitting procedure is interactive (msf), and fits these scalings with rational, stable transfer function matrices, .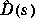

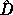After fitting, plots of

and

are shown for comparison.

3.: (In the 1st iteration, this step is skipped.) The rational is absorbed into the open-loop interconnnection for the next controller synthesis. Using either (based on GMAX_DK_PLAN, see below) the previous frequency-dependent D's or the just-fit rational 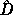, an estimate of an appropriate value for GMAX_DK is made. This is simply a conservative value of the scaled closed- loop H norm, using the most recent controller and either a frequency sweep (using the frequency-dependent Ds) or a state-space calculation (with the rational D's).

4.: (In the 1st iteration, this step is skipped.) The parameters that will be used in the upcoming hinfsyn are displayed. It is your option to change any/all/ none of these.

5.: (The 1st iteration begins at this point.) A controller is designed using H synthesis on the scaled open-loop interconnection.

The progress of the -iteration is displayed.
The singular values of the closed-loop frequency response are plotted.
You are given the option to change the frequency range (OMEGA_DK). If you change it, all relevant frequency responses are automatically recomputed.
You are given the option to rerun the H synthesis with modified hinfsyn parameters. This is convienient if, for instance, the bisection tolerance was too large, or if GMAX_DK was too small.

6.: Using the block structure BLK_DK, bounds for the structured singular value of the closed-loop system are calculated and plotted.

7.: An iteration summary is displayed, showing all of the controller order, as well as the peak value of µ of the closed-loop frequency responses.

8.: The choice of stopping, or performing another iteration is given.

Subsequent iterations proceed along the same lines without the need to re-enter the iteration number. A summary at the end of each iteration is updated to reflect data from all previous iterations. This often provides valuable information about the progress of the robust controller synthesis procedure.

To continue iterating on a problem that was started earlier, make sure the relevent data is in the workspace, run dkit and type the number of the iteration you would like to begin.

The following is a list of the variables that you must set (in either dk_defin file or the file defined by DK_DEF_NAME) and their meanings:

NOMINAL_DK
Nominal plant interconnection structure, a µ-Tools SYSTEM matrix.

NMEAS_DK
Number of sensor measurements.

NCONT_DK
Number of control inputs.

BLK_DK
Block structure forµ calculation, used by mu.

OMEGA_DK
Frequency response range.

`NOMINAL_DK`	Nominal plant interconnection structure, a µ-Tools SYSTEM matrix.
`NMEAS_DK`	Number of sensor measurements.
`NCONT_DK`	Number of control inputs.
`BLK_DK`	Block structure forµ calculation, used by `mu`.
`OMEGA_DK`	Frequency response range.

The following is a list of the optional variables that may be set (in either dk_defin file or the file defined by DK_DEF_NAME) and their meanings:

GMIN_DK
Lower bound for first H controller design

GMAX_DK
Upper bound for first H controller design

GTOL_DK
H bisection tolerance for first iteration

GMAX_DK_PLAN
Estimates for GMAX_DK in subsequent iterations are made in three manners. The value of GMAX_DK_PLAN determines which formula is used:

0 Use previous GMAX_DK

1 use 1.2*pkvnorm(peak_mu_value)

2 use hinfnorm(mmult(dsysL,clp,minv(dsysR)))

`GMIN_DK`	Lower bound for first H controller design
`GMAX_DK`	Upper bound for first H controller design
`GTOL_DK`	H bisection tolerance for first iteration
`GMAX_DK_PLAN`	Estimates for `GMAX_DK` in subsequent iterations are made in three manners. The value of `GMAX_DK_PLAN` determines which formula is used:
	0 Use previous `GMAX_DK`
	1 use `1.2*pkvnorm(peak_mu_value)`
	2 use `hinfnorm(mmult(dsysL,clp,minv(dsysR)))`

A number of variables are saved in the workspace after each iteration. Some of these variables are required every iteration, hence, it doesn't make sense to recompute them. The other variables are outputs from the D-K iteration procedure. The variables saved after each iteration are:

bnds_dk(i)
Frequency domain upper and lower bounds for µ associated with the ith iteration. The (i) denotes the ith iteration which is augmented to the name by the program dkit.

dl_dk(i)
Left state-space D-scale associated with ith iteration. The (i) denotes the ith iteration which is augmented to the name by the program dkit. Hence, dl_dk5 would be the left state-space D-scale from the fifth iteration.

dr_dk(i)
Right state-space D-scale associated with ith iteration. Same notation.

Dscale_dk(i)
D-scaling data output from mu associated with ith iteration. Dscale_dk(i) is in compressed form. Same notation.

gf_dk(i)
The H norm of the ith iteration closed-loop system. Same notation.

k_dk(i)
Controller from the ith iteration. Same notation.

nom_dk_g
Frequency response of NOMINAL_DK using OMEGA_DK.

sens_dk(i)
Sensitivity data output from the ith iteration mu calculation. Same notation.

`bnds_dk(i)`	Frequency domain upper and lower bounds for µ associated with the ith iteration. The (i) denotes the ith iteration which is augmented to the name by the program `dkit.`
`dl_dk(i)`	Left state-space D-scale associated with ith iteration. The (i) denotes the ith iteration which is augmented to the name by the program `dkit`. Hence, `dl_dk5` would be the left state-space D-scale from the fifth iteration.
`dr_dk(i)`	Right state-space D-scale associated with ith iteration. Same notation.
`Dscale_dk(i)`	D-scaling data output from `mu` associated with ith iteration. `Dscale_dk(i)` is in compressed form. Same notation.
`gf_dk(i)`	The H `norm` of the ith iteration closed-loop system. Same notation.
`k_dk(i)`	Controller from the ith iteration. Same notation.
`nom_dk_g`	Frequency response of `NOMINAL_DK` using `OMEGA_DK`.
`sens_dk(i)`	Sensitivity data output from the ith iteration `mu` calculation. Same notation.

Fitting D-scalings
The D-scale fitting procedure is interactive and uses the µ-Tools command msf. During step 2 of the D-K iteration procedure, you are prompted to enter your choice of options for fitting the D-scaling data. After pressing return, the following is a list of your options.

Enter Choice (return for list):
Choices:
nd          Move to Next D-Scaling
nb          Move to Next D-Block
i           Increment Fit Order
d           Decrement Fit Order
apf         Auto-PreFit
mx 3        Change Max-Order to 3
at 1.01     Change Auto-PreFit tol to 1.01
0           Fit with zeroth order
2           Fit with second order
n           Fit with n'th order
e           Exit with Current Fittings
s           See Status

nd and nb allow you to move from one D-scale data to another. nd moves to the next scaling, whereas nb moves to the next scaling block. For scalar D-scalings, these are identical operations, but for problems with full D-scalings, (perturbations of the form 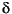I) they are different. In the (1,2) subplot window, the title displays the D-scaling Block number, the row/column of the scaling that is currently being fit, and the order of the current fit (with d for data, when no fit exists).
The order of the current fit can be incremented or decremented (by 1) using i and d.
apf automatically fits each D-scaling data. The default maximum state order of individual D-scaling is 5. The mx variable allows you to change the maximum D-scaling state order used in the automatic prefitting routine. mx must be a positive, nonzero integer. at allows you to define how close the rational, scaled µ upper bound is to approximate the actual µ upper bound in a norm sense. Setting at 1 would require an exact fit of the D-scale data, and is not allowed. Allowable values for at are greater than 1. This setting plays a role (mildly unpredictable, unfortunately) in determining where in the (D,K) space the D-K iteration converges.
Entering a positive integer at the prompt will fit the current D-scale data with that state order rational transfer function.
e exits the D-scale fitting to continue the D-K iteration.
The variable s will display a status of the current and fits.

Examples
An example of using dkit for D-K iteration is provided in the "HIMAT Robust Performance Design Example" in Chapter 7.

Reference
Balas, G.J.and J.C. Doyle, "Robust control of flexible modes in the controller crossover region," AIAA Journal of Guidance, Dynamics and Control, Vol. 17, no. 2, pp. 370-377, March-April, 1994.

Balas, G.J., A.K. Packard and J.T. Harduvel, "Application of µ-synthesis techniques to momentum management and attitude control of the space station," AIAA Guidance, Navigation and Control Conference, New Orleans, August 1991.

Doyle, J.C., Doyle, K. Lenz, and A. Packard, "Design examples using µ-synthesis: Space shuttle lateral axis FCS during reentry," NATO ASI Series, Modelling, Robustness, and Sensitivity Reduction in Control Systems, vol. 34, Springer-Verlag, 1987.

Packard, A., J. Doyle, and G. Balas, "Linear, multivariable robust control with a µ perspective," ASME Journal of Dynamic Systems, Measurement and Control, 50th Anniversary Issue, vol. 115, no. 2b, pp. 310-319, June 1993.

Stein, G., and J. Doyle, "Beyond singular values and loopshapes," AIAA Journal of Guidance and Control, vol. 14, no. 1, pp. 5-16, January, 1991.

See Also
hinfsyn, hinfnorm, msf, mu

dhfsyn dkitgui