genmu (Mu Analysis and Synthesis Toolbox)

Mu Analysis and Synthesis Toolbox

genmu

Compute upper bounds for the mixed (real and complex) generalized structured singular value (referred to as generalized mixed µ) of a VARYING/CONSTANT matrix

Syntax

```
[bnd,dvec,gvec,qmat] = genmu(M,C,blk);
```

Description
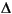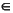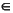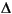
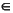
Generalized µ allows us to put additional constraints on the directions that I - M becomes singular. Given a matrix M Cnxn, and C Cmxn, find the smallest (described by blk) such that

is not full column rank. Specifically, define

This quantity can be bounded above, using standard µ ideas. If there exists a matrix Q such that

µ_D(M + QC) <

then µ_D(M,C) < . Hence,

It is possible to compute the optimal matrix Q which minimizes the standard µ upper bound for µ_D(M + QC). The optimization problem can be reformulated into an affine matrix inequality, [PacZPB], and solved with a combination of heuristics and general purpose AMI solvers. This is how genmu computes the upper bound µ_D(M,C).

The upper bound for µ_D(M,C) is returned in bnd. The scaling matrices D and G associated with the upper bound are in packed format, in the matrics dvec and gvec, and can be unwrapped with muunwrap. The Q matrix which mimimizes the bound is returned in qmat. If either M or C are VARYING matrices, then the bound is computed at each value of the independent variable, and the output matrices (bnd, dvec, gvec and qmat) are also VARYING matrices.

Reference
Pachard, A., K. Zhou, P. Pandey, and G. Becker, "A collection of robust control problems leading to LMI's," 30th IEEE Conference on Decision and Control, pp. 1245-1250, Brighton, UK, 1991.

See Also
cmmusyn, mu

gap, nugap getiv, sortiv, tackon