Mu Analysis and Synthesis Toolbox

dypert operates on output from a VARYING mu (µ) calculation to construct a worst-case, real-rational, stable perturbation

sisorat constructs a first-order, real-rational, stable, all-pass transfer function that interpolates a particular complex number at a given, positive frequency.

Syntax

• pert = dypert(pvec,blk,bnds); 
  pert = dypert(pvec,blk,bnds,blkindex); 
  ratfit = sisorat(value);
  

Description
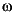The input to dypert consists of the perturbation pvec, the block structure blk, and lower and upper bounds, bnds, produced from a VARYING matrix µ calculation. (See the µ-Tools command mu for a more complete description of these variables.) By searching in bnds, dypert finds the peak value of the lower bound -- for example , occurring at frequency ₀. dypert then extracts the perturbation (call this matrix 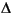₀) from pvec at the frequency 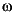₀. dypert constructs a SYSTEM matrix, pert, which is stable, and has the block-diagonal structure associated with blk, and also satisfies the equations:

The command dypert can also be called with four input arguments. In this case, the last argument is a vector of integers. This vector, blkindex, specifies which blocks in the perturbation structure specified by the blk vector, are to be used to construct the rational perturbation. For instance, if the block structure specified by blk is

and the fourth argument to dypert is [3 6 4 1] (indicating first, third, fourth, and sixth blocks are desired), then the output SYSTEM matrix produced by dypert will be a SYSTEM matrix that looks like

This is useful when some of the perturbations are not physical perturbations, but correspond to performance objectives, and hence do not need to be constructed. Note that regardless of the order in which the numbers occur in the fourth argument, the perturbations in the output SYSTEM pert are in ascending order. When dypert is called with three arguments, all the perturbations are constructed.

The command sisorat is essentially a scalar version of dypert, and is the main subroutine for dypert. The input to sisorat is value, a 1 x 1, VARYING matrix, with one independent variable value. The independent variable is interpreted as a frequency, 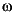₀, and the numerical value of value at that frequency is denoted by . The output of sisorat is a single-input/single-output stable, real, SYSTEM matrix, ratfit, satisfying:

Algorithm
The main subroutine of dypert is sisorat, which operates on the following fact: for any complex number , and any real frequency 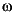₀ > 0, there is a real number 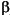> 0 such that by proper choice of sign, the equality

holds. This is exactly how sisorat works.

In order to understand how dypert works, recall in Chapter 4, the section "Complex Structured Singular Value," Remark 1 after Definition 2.1. There it was shown that each full block of a perturbation that causes singularity can in fact be chosen to be a dyad, and the program mu does this at each independent variable value. Hence, the matrix 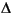₀, as described above, is a diagonal augmentation of scalar blocks, and dyads. Given that the ith block is a dyad, write it as 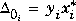for complex vectors yi and xi. Using several calls to sisorat, it is possible to create two stable, rational vectors h(s) (column) and r(s) (row), such that each element of the vectors is of the form generated by sisorat (stable, and flat across frequency), and for each k and l

If we define 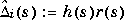then it is stable, and

Performing this on a block-by-block basis produces the entire rational perturbation. For the case of a repeated scalar block, that part of the perturbation is constructed directly with one call to sisorat and diagonally augmented as many times as needed.

See Also
mu, randel, svd, vsvd

drawmag

fitmag, genphase, fitmaglp, magfit