Mu Analysis and Synthesis Toolbox

Create a sample-hold approximation of a continuous system

Syntax

• discout = samhld(sys,T)
  

Description
samhld applies a sample-hold to the input of the continuous-time systems sys, and samples the output, to produce a discrete-time system, discout. The sampling time is the same at the input and output, and is specified by T.

Examples
Construct the system sys via the nd2sys command and verify that all of its poles are in the closed left-half plane. Perform a sample hold of the system for a 200 Hz sample rate. All the poles for the discretized system, discout, are within the unit disk.

• sys = nd2sys([1 2 4 5],[2 7 9 2]); 
  spoles(sys)
  -1.6114 + 1.0049i
  -1.6114 - 1.0049i
  -0.2773
  discout = samhld (sys ,1 / 2 0 0)
  seesys (discout, '%8 .4f ')
  
  0.9826    -0.0223   -0.0050  |  0.0050
  o.0050     0.9999   -0.0000  |  0.0000
  0.0000     0.0050    1.0000  |  0.0000
  -----------------------------|---------
  -0.7500    -0.2500   2.0000  |  0.5000
  
  spoles(discout)
  
  0.9920 + 0.0050i
  0.9920 - 0.0050i
  0.9986
  

Algorithm
Suppose that the continuous-time system has state-space representation

If u(t) is held constant over the interval [kT,(k + 1)T], then over that interval, the state evolution is governed by the differential equation

which captures the behavior of the continuous-time system, over one sample period, while the input u(t) is held constant.

Let 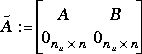. Define


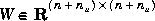
as 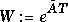. Then W appears as

Define A_disc := W₁₁, and B_disc := W₁₂, and define the discretized system as

See Also
exp, expm, tustin

rifd

scliv