Mu Analysis and Synthesis Toolbox    
hinfsyne

Compute an H controller for a SYSTEM interconnection matrix that minimizes the entropy integral at a specific frequency

Syntax

Description
hinfsyne is a variation of hinfsyn and calculates an H controller that achieves the infinity norm gfin for the interconnection structure p. The controller, k, stablizes the SYSTEM matrix p and has the same number of states as p. Of the controllers achieving this norm bound, k is chosen to minimize an entropy integral relating to the point s0; i.e.,

where g is the closed-loop transfer function. In addition, the amount of printing on the screen can be controlled.

Input arguments:

p
 SYSTEM interconnection structure matrix
nmeas
 number of measurements output to controller
ncon
 number of control inputs
gmin
 lower bound on
gmax
 upper bound on
tol
     relative difference between final values
s0
 point at which entropy is evaluated (default )
quiet
 controls printing on the screen
 1 no printing
 1 header not printed
-1 full printing (default)
ricmethod
  1 Eigenvalue decomposition with balancing
-1 Eigenvalue decomposition with no balancing
 2 Schur decomposition with balancing (default)
-2 Schur decomposition with no balancing
epr
 measure of when a real part of an eigenvalue of the Hamiltonian matrix is zero (default epr = 1e-10)
epp
 positive definite determination of the X and Y solution (default epp = 1e-6)

Output arguments:

k
 H (sub) optimal controller
g
 closed-loop system with H controller
gfin
 final value achieved
ax
 X Riccati solution as a VARYING matrix with independent variable
ay
 Y Riccati solution as a VARYING matrix with independent variable
hamx
 H Hamiltonian matrix as a VARYING matrix with independent variable
hamy
 J Hamiltonian matrix as a VARYING matrix with independent variable

Note that the outputs ax, ay, hamx, and hamy correspond to scaled or balanced data.

The hinfsyne program outputs several variables, which can be checked to ensure that the above conditions are being met. For each 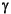value the minimum magnitude, real part of the eigenvalues of the X Hamiltonian matrices is displayed along with the minimum eigenvalue of X, which is the solution to the X Riccati equation. A # sign is placed to the right of the condition that failed in the printout. This additional information can aid you in the control design process.

Algorithm
hinfsyne uses the formulas similar to the ones described in the Glover and Doyle paper for solution to the H control design problem. See the hinfsyn command for more information.

Subroutines called.    hinf_st, hinf_gam, hinfe_c, hinf_gam calls: ric_eig, ric_schr, csord, and cgivens

Reference
Doyle, J.C., K. Glover, P. Khargonekar, and B. Francis, "State-space solutions to standard H2 and H control problems," IEEE Transactions on Automatic Control, vol. 34, no. 8, pp. 831-847, August 1989.

Glover, K., and J.C. Doyle, "State-space formulae for all stabilizing controllers that satisfy an Hnorm bound and relations to risk sensitivity," Systems and Control Letters, vol. 11, pp. 167-172, 1988.

See Also
dhfsyn, hinfsyn, hinffi, hinfnorm, h2syn, h2norm, ric_eig, ric_schr, sdhfsyn


hinfsyn indvcmp