Mu Analysis and Synthesis Toolbox

Compute H full-information controller for a SYSTEM interconnection matrix

Syntax

• [k,g,gfin,ax,hamx] = 
                         hinffi(p,ncon,gmin,gmax,tol,ricmethd,epr,epp)
  

Description
hinffi calculates an H full information controller that achieves the infinity norm gfin for the interconnection structure p. The controller, k, stablizes the SYSTEM matrix p and is constant gain. The system p is partitioned:

where B₁ are the disturbance inputs, B₂ are the control inputs, and C₁ are the errors to be kept small. B₂ has the column size ncon. Within the hinffi program, the SYSTEM matrix p is augmented with state and disturbance measurements; i.e., the identity matrix with size equal to the number of states of p and the identity matrix with size equal to the number of disturbances. Be careful when closing the loop with the full information controller since the extra measurements are only augmented inside the command hinffi. The internal system used for control design is

The controller is returned in k and the closed-loop system is returned in g. The program provides a iteration using the bisection method. Given a high and low value of , gmax and gmin, the bisection method is used to iterate on the value of in an effort to approach the optimal full information H control design. If gmax = gmin, only one value is tested. The stopping criteria for the bisection algorithm requires the relative difference between the last value that failed and the last value that passed be less than tol. You can select either the eigenvalue or Schur method with or without balancing for solving the Riccati equations. The eigenvalue method is faster but can have numerical problems, while the Schur method is slower but generally more reliable.

The algorithm employed requires tests to determine whether a solution exists for a given value. epr is used as a measure of when the Hamiltonian matrix has imaginary eigenvalues and epp is used to determine whether the Riccati solution is positive semi-definite. The selection of epr and epp should be based on your knowledge of the numerical conditioning of the interconnection structure p. The conditions checked for the existence of a solution are

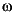• H Hamiltonian matrix must have no j-axis eigenvalues
• the stabilizing solution, X, of the associated Riccati equation must exist, and be must be positive, semi-definite.

p	SYSTEM interconnection structure matrix
ncon	number of controller outputs
gmin	lower bound on
gmax	upper bound on
tol	relative difference between final values, iteration stopping criteria
ricmethd	1 Eigenvalue decomposition with balancing. -1 Eigenvalue decomposition with no balancing  2 Schur decomposition with balancing (default) -2 Schur decomposition with no balancing
epr	measure of when a real eigenvalue of the Hamiltonian matrix is zero (default epr = 1e-10, optional)
epp	positive definite determination of the X solution (default epp = 1e-6, optional)

Output arguments

k	H full information controller
g	closed-loop system with H full information controller
gfin	final achieved
ax	Riccati solution as a VARYING matrix with independent variable
hamx	Hamiltonian matrix as a VARYING matrix with independent variable

:

Note that the outputs ax, ay, hamx, and hamy may correspond to scaled or balanced data. The following assumptions are made in the implementation of the hinfsyn algorithm and must be satisfied:

(i) (A,B₂) is stabilizable

(ii) D₁₂ is full column rank

(iii)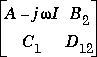 has full column rank for all .

where denotes the frequency variable.

On return, there must be no j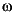-axis eigenvalues associated with the H Hamiltonian matrices and the eigenvalues of the Riccati solution, X, must all be 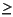0, for the closed-loop system to be stable and to have an H norm less than . The bisection algorithm iterates on the value of to approach the optimal H full information controller.

The hinffi program outputs several variables, which can be checked to ensure that the above conditions are being met. For each value the minimum magnitude, real part of the eigenvalues of the H Hamiltonian matrices is displayed along with the minimum eigenvalue of X, which is the solution to the Riccati equation. A # sign is placed to the right of the condition that failed in the printout.

Examples
Given an interconnection structure sys with one control input, it is desired to synthesize a full information controller. The upper bound on is 1.0 and the lower bound is specified as 0.1. A tolerance of 0.02 is selected for the stopping condition for the iteration and the Schur method is used to solve the Riccati equations. The command hinffi outputs the display shown for each value of . The final value achieved is 0.2547.

• ncont = 1;% number of control inputs 
  gmin = .1;% minimum gamma value to be tested 
  gmax = 1;% maximum gamma value to be tested 
  tol = .02;% tolerance on the gamma stopping value 
  ricmethd = 2;% Riccati solution via the Schur method 
  seesys(p)% plant interconnection structure
  

• 3    1  |   4
  0    0  |   1
  -------------
  1    0  |   0
  
  [k,g,gf,ax,hx] = hinffi(p,1,.1,1,.02,2);
  Test bounds:0.1000<   gamma<=1.0000
  gamma       ham_eig       x_eig         pass/fail
  1.000       4.90e+00      5.27e-01      pass
  0.550       4.66e+00      6.03e-01      pass
  0.325       3.94e+00      1.06e+00      pass
  0.213       1.69e+00     -7.63e-01#     fail
  0.269       3.34e+00      2.94e+00      pass
  0.241       2.78e+00     -4.55e+00#     fail
  0.255       3.10e+00      1.04e+01      pass
  
  Gamma value achieved:0.2547
  

Algorithm
hinffi uses the formulas similar to the ones described in the Glover and Doyle, 1988 paper for solution to the H control design problem. See the hinfsyn command for more information.

hinffi_g calls: ric_eig, ric_schr, csord, and cgivens

Reference
Doyle, J.C., K. Glover, P. Khargonekar, and B. Francis, "State-space solutions to standard H₂ and H control problems," IEEE Transactions on Automatic Control, vol. 34, no. 8, pp. 831-847, August 1989.

Glover, K., and J.C. Doyle, "State-space formulae for all stabilizing controllers that satisfy an H norm bound and relations to risk sensitivity," Systems and Control Letters, vol. 11, pp. 167-172, 1988.

See Also
h2syn, h2norm, hinfsyn, hinfsyne, hinfnorm, ric_eig, ric_schr

h2syn

hinfsyn