Mu Analysis and Synthesis Toolbox

gap calculates the gap metric between two SYSTEM matrices

nugap calculates the 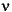gap between two SYSTEM matrices.

Syntax

• gap = gap(sys1,sys2, ttol)
  

Description
gap and nugap compute the gap and 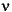gap metrics between two SYSTEM matrices. Both quantities give a numerical value 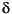(G₀,G₁) between 0 and 1 for the distance between a nominal system sys1 (G₀) and a perturbed system sys2 (G₁). The gap metric was introduced into the control literature by Zames and El-Sakkary, 1980, and exploited by Georgiou and Smith, 1990. The 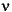gap metric was derived by Vinnicombe, 1993. For both of these metrics the following robust performance result holds from Qui and Davidson, 1992, and Vinnicombe, 1993:

arcsin b(G₁,K₁) 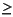arcsin b(G₀,K₀)- arcsin 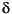(G₀,G₁)- arcsin 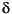(K₀,K₁)

where

The interpretation of this result is that if a nominal plant G₀ is stabilized by controller K₀, with "stability margin" b(G₀,K₀), then the stability margin when G₀ is perturbed to G₁ and K₀ is perturbed to K₁ is degraded by no more than the above formula. Note that 1/b(G,K) is also the signal gain from disturbances on the plant input and output to the input and output of the controller. The 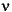gap is always less than or equal to the gap, so its predictions using the above robustness result are tighter. To make use of the gap metrics in robust design, weighting functions need to be introduced. In the above robustness result, G needs to be replaced by W₂GW₁ and K by 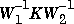(similarly for G₀, G₁, K₀ and K₁). This makes the weighting functions compatible with the weighting structure in the "Loop Shaping Using H· Synthesis" section in Chapter 3. Model reduction of the system model and controller can be performed by using balanced truncations or Hankel norm approximation of normalized coprime factor representations.

ttol defines the tolerance to which the gap is computed. The default is 0.001.

Algorithm
Tryphon Georgiou and Malcolm Smith wrote the gap program.

The computation of the gap amounts to solving 2-block H-problems, Georgiou, 1988. The particular method used here for solving the H-problems is based on Green et al., 1990. The computation of the nugap uses the method of Vinnicombe, 1993.

Reference
Georgiou, T.T., On the computation of the gap metric, Systems Control Letters, vol. 11, pp. 253-257, 1988.

Georgiou, T.T., and M. Smith, "Optimal robustness in the gap metric," IEEE Transactions on Automatic Control, vol. 35, pp. 673-686, 1990.

Green, M., K. Glover, D. Limebeer, and J.C. Doyle, "A J-spectral factorization approach to H control," SIAM J. of Control and Opt., 28(6), pp. 1350-1371, 1990.

Qiu, L., and E.J. Davison, "Feedback stability under simultaneous gap metric uncertainties in plant and controller," Systems Control Letters, vol. 18-1, pp. 9-22, 1992.

Vinnicombe, G., "Measuring Robustness of Feedback Systems," PhD dissertation, Department of Engineering, University of Cambridge, 1993.

Zames, G., and El-Sakkary, "Unstable systems and feedback: The gap metric," Proceedings of the Allerton Conference, pp. 380-385, Oct., 1980.

See Also
dhfnorm, emargin, hinfnorm, ncfsyn, mu

frsp

genmu