Mu Analysis and Synthesis Toolbox

Compute the optimal H₂ controller given a SYSTEM interconnection matrix

Syntax

• [k,g,norms,kfi,gfi,hamx,hamy] =h2syn(p,nmeas,ncon,ricmethod)
  

Description
h2syn calculates the H₂ optimal controller k and the closed-loop system g for the linear fractional interconnection structure p. nmeas and ncon are the dimensions of the measurement outputs from p and the controller inputs to p. The optional fourth argument, ricmethod, determines the method used to solve the Riccati equations. The interconnection structure, p, is defined by

Input arguments

p	SYSTEM interconnection structure matrix
nmeas	number of measurements output to controller
ncon	number of control inputs
ricmethd	1 Eigenvalue decomposition with balancing -1 Eigenvalue decomposition with no balancing 2 Schur decomposition with balancing. (default) -2 Schur decomposition with no balancing.

Output arguments

k	H2 optimal controller
g	closed-loop system with optimal controller
norms	norms of four different quantities, full information control cost (FI), output estimation cost (OEF), disturbance feedforward cost (DFL) and full control cost (FC), norms = [FI OEF DFL FC];
kfi	full information/state feedback control law
gfi	full information/state feedback closed-loop system
hamx	H2 Hamiltonian matrix
hamy	H2 Hamiltonian matrix

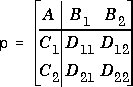
The equations and corresponding nomenclature are taken from the Doyle, et al., 1989, reference. The full information cost is given by the equation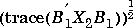 The output estimation cost is given by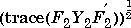, where 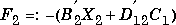. The disturbance feedforward cost is 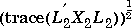, where L₂ is defined by 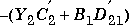and the full control cost is given by 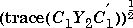. X₂ and Y₂ are the solutions to the X and Y Riccati equations, respectively.

The H₂ solution provides an upper bound on for use in the hinfsyn program.

Examples
Design an H₂ optimal controller for a system matrix, himat_icn, with two sensor measurements (nmeas), two error signals, two actuator inputs (ncont), and eight states. himat_icn differs from the SYSTEM interconnection structure himat_ic by the fact that the D₁₁ term of himat_ic is set to be zero. The Schur decompostion method, ricmethd = 2, will be used for solution of the Riccati equations. The program outputs the minimum eigenvalue of X₂ and Y₂ during the computation.

• nmeas = 2; 
  ncont = 2; 
  ricmethd = 2; 
  minfo(himat_icn)
  system:8 states6 outputs6 inputs
  [k,g] = h2syn(himat_icn,nmeas,ncont,ricmethd);
  minimum eigenvalue of X2: 2.260000e-02
  minimum eigenvalue of Y2: 2.251670e-02
  

• hinfnorm(g)
  norm between 2.787 and 2.79
  achieved near 29.9
  h2norm(g)
  1.594e+01
  

Algorithm
h2syn is an M-file in µ-Tools that uses the formulae described in the Doyle, et al., 1989, reference for solution to the optimal H₂ control design problem. A Hamiltonian is formed and solved via a Riccati equation (ric_eig and ric_schr). The D matrix associated with the input disturbances and output errors is restricted to be zero.

Reference
Doyle, J.C., K. Glover, P. Khargonekar, and B. Francis, "State-space solutions to standard H₂ and H control problems," IEEE Transactions on Automatic Control, vol. 34, no. 8, pp. 831-847, August 1989.

Glover, K., and J.C. Doyle, "State-space formulae for all stabilizing controllers that satisfy an H norm bound and relations to risk sensitivity," Systems and Control Letters, 1988. vol. 11, pp. 167-172, August 1989.

See Also
hinfsyn, hinffi, h2norm, hinfnorm, ric_eig, ric_schr

h2norm, hinfnorm

hinffi