| Mu Analysis and Synthesis Toolbox | |
Solve a Riccati equation via Schur decomposition
Syntax
Description
ric_schr (along with a call to x=x2/x1) solves the Riccati equation,
such that A + RX is stable. A real Schur decomposition can obtain the stable invariant subspace of the Hamiltonian matrix, ham. The data matrices A, R, and Q come from the input Hamiltonian matrix in the form
and it is assumed that and it is assumed that R = R', Q = Q'.
If ham has no j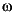
axis eigenvalues, then there exists n x n matrices x1 and x2 such that [x1; x2] spans the n-dimensional stable, invariant subspace of ham. If x1 is invertible, then X := x2 * x1-1 satisfies the Riccati equation and results in A + RX being stable. The output flag fail is nominally 0. If there are j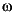-axis eigenvalues, fail is set to 1. If there are an unequal number of positive and negative eigenvalues, fail is set to 2, and if both conditions occur, fail = 3.
Algorithm
ric_schr calls csord to produce an ordered complex Schur form, which is converted to a real Schur form, and yields a stable, invariant subspace of the Hamiltonian. The csord command orders the solution with negative real eigenvalues in the top half of the matrix and the positive real eigenvalues on the bottom, and returns the stable solution. The input matrix is assumed to be a Hamiltonian matrix of size 2n with n stable eigenvalues and n unstable eigenvalues. The minimum real part of the eigenvalues is output to reig_min. epp is an optional argument and its default value is 1e-10.
See Also
csord, h2syn, hinfsyn, hinffi, ric_eig, schur
| ric_eig | rifd | |
