

| Mu Analysis and Synthesis Toolbox |   |
Calculate the balanced realization and optimal Hankel norm approximation of a SYSTEM matrix. sysbal and hankmr are restricted to be used on continuous-time SYSTEM matrices whose poles have negative real part
Syntax
Description
sysbal performs a truncated balanced realization of the input SYSTEM matrix. The result is truncated to retain all Hankel singular values greater than tol. If tol is omitted then it is set to
max(hanksv(1) * 1.0-12,1.0-16)
The second output argument of sysbal is the vector hanksv, which contains the Hankel singular values of the input system, sys. One method to get a reduced-order model is to truncate the balanced system sysb using strunc.
hankmr returns sysred, the optimal Hankel norm approximation of order k to the SYSTEM matrix, sysb, which is a balanced realization with Hankel singular values hanksv and is of order n (n > k). The fourth optional input argument, opt, may be omitted in which case sysanti contains the anti-causal term such that the L norm of
norm of (sysb - sysred - sysanti) is hanksv(k+1) or set to:
'a' when sysout also includes the anti-casual term, and sysanti=0
'd' when sysout includes a D matrix to reduce the H error norm of (
error norm of (sys - sysout)
If the d option is set, the third output argument of hankmr is the vector siganti, which contains the Hankel singular values of the system, sysanti~. In this case
Examples
Given the system 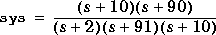 , reduce the system to two and one states, respectively. First reduce the system to two states.
, reduce the system to two and one states, respectively. First reduce the system to two states.
sys = zp2sys([-10 -90],[-2 -91 -100]); w = logspace(-1,3,100); sysg = frsp(sys,w); [syssb,sv]=sysbal(sys); sv ans = 2.0613e-024.1136e-031.2663e-06 sys2s =strunc(syssb,2); sys2sg =frsp(sys2s,w); sys2h =hankmr(syssb,sv,2); sys2hg =frsp(sys2h,w);vplot('bode',sys_g,sys2sg,sys2hg) tmp = 'Original 3 state system, 2 state Balanced '; tmp1= 'and Hankel Model Reduction'; title([tmp tmp1])
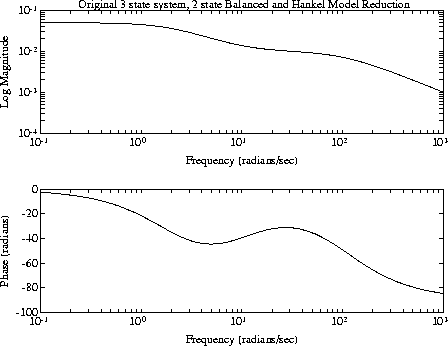
sysbal and hankmr.
sys1s =strunc(syssb,1);sys1sg =frsp(sys1s,w);sys1h =hankmr(syssb,sv,1);sys1hg =frsp(sys1h,w); [syssb,sv] =sysbal(sys);vplot('bode',sys_g,sys1sg,sys1hg) tmp = 'Original 3 state system, 1 state Balanced ' tmp1= 'and Hankel Model Reduction') title([tmp tmp1])
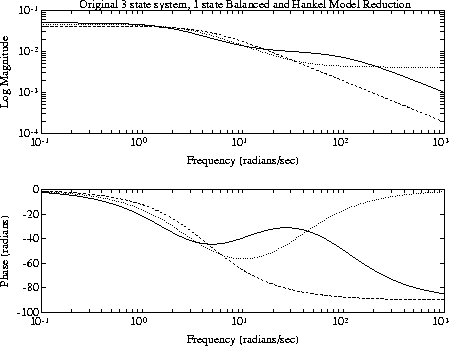
The original three state system corresponds to the solid line, the one state balanced realization system corresponds to the dashed line, and the one state Hankel model reduced system corresponds to the dotted line. There is significant differences between the models and the two model reduction techniques. Depending on the model reduction objectives, the one state models may be inappropriate for use.
Reference
K. Glover, "All optimal Hankel-norm approximations of linear multivariable systems and their error bounds," International Journal of Control, vol. 39, pp. 1115-1193, 1984.
See Also
sdecomp, sfrwtbal, sfrwtbld, sresid, srelbal, sresid
 | statecc, strans | sysic |  |