| Getting Started | |
線形二次ガウシアン(LQG)設計
LQG制御は、最適ダイナミックレギュレータを設計する、近代的な状態空間手法です。これは、レギュレータの性能と制御に使用する事柄とのトレードオフを行い、プロセスノイズや測定ノイズを利用するものです。極配置と同様に、LQG設計は、プラントの状態空間モデルを必要とします(関数ssを使って、他のLTIモデルから状態空間モデルに変換)。この節は、連続時間系のみを取り扱います(離散時間のLQG設計の詳細は、関連したリファレンスを参照してください)。
目的は、出力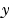
をゼロ近傍にレギュレーションすることです。プラントはプロセスノイズ
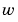と制御
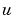で駆動し、レギュレータは、これらの制御を行うノイズの測定量
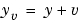に依存します。プラントの状態と測定方程式は、つぎのようになります。
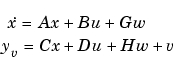
LQGレギュレータは、最適状態フィードバックゲインとKalman状態エスティメータから構成されています。つぎに示すように、これら二つの補償器を独立に設計できます。
最適状態フィードバックゲイン
LQG制御で、レギュレーション問題は、つぎの二次型の性能規範で判断します。
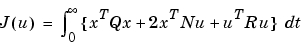
重み付き行列、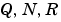
は、レギュレーション性能(如何に速く、
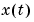をゼロに近づけるか)とそれに対する制御操作とのトレードオフを設定するものです。
最初の設計は、評価関数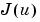
.を最小にする状態フィードバック則
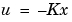を求めることです。最小化されたゲイン行列 は、代数Riccati方程式を解くことで得られます。このゲインをLQ-最適ゲインと云います。
Kalman状態エスティメータ
極配置の場合と同じように、LQ-最適状態フィードバック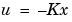
は、全状態測定がなければ実現しません。しかし、出力フィードバック問題に対して、
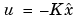が最適であるような状態推定
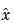を引き出すことは可能です。この状態推定は、Kalmanフィルタで作成できます。
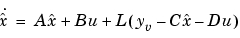
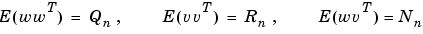
は、代数Riccati方程式を使って、Kalmanゲイン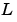 
を決定します。
Kalmanフィルタは、ガウシアン白色ノイズを取り扱う場合、最適エスティメータになります。特に、エスティメータの誤差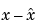 
の漸近的な共分散
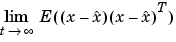
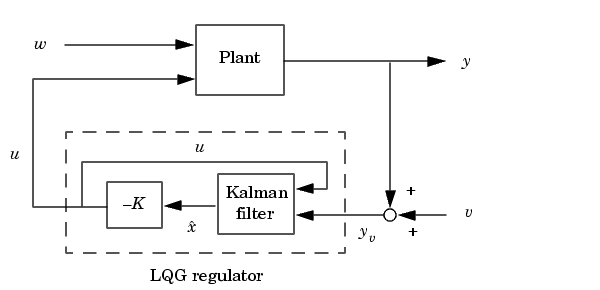
LQGレギュレータ
LQGレギュレータを作成するためには、つぎに示すように、KalmanフィルタとLQ-最適ゲイン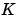
を単に結合してください。
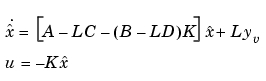
LQG設計ツール
Control System Toolboxは、上述した3つのLQG設計ステップを実現する関数を用意しています。これらの関数は、連続系プラントに対して、離散のLQGレギュレータを設計することと同様に、連続系、離散系の問題を共に解くことができます。
| LQG設計 | |
|
連続時間代数Riccati方程式を解く |
|
離散時間代数Riccati方程式を解く |
|
離散システムに対するLQ-最適ゲイン |
|
Kalmanエスティメータ |
|
連続プラント用の離散のKalmanエスティメータ |
|
LQゲインとKalmanフィルタを与えて、LQGレギュレータを作成 |
|
連続システム用のLQ-最適ゲイン |
|
連続プラント用の離散LQゲイン |
|
出力に重み付けを行ったLQ-最適ゲイン |
LQG設計の例題に対して、Help Deskの中のケーススタディオンラインのLQGケーススタディを参照してください。Kalmanフィルタを操作するには、関数kalmanとkalmdを使うこともできます。詳細は、ケーススタディの、Kalmanフィルタのケーススタディを参照してください｡
| | 極配置 | さらに、学ぶため | |
と
が共に、白色ノイズと考えます。
(制御)と
(測定)です。ノイズの共分散データ