

| Control System Toolbox関数リファレンス |   |
表示
[X,L,G,rr] = dare(A,B,Q,R) [X,L,G,rr] = dare(A,B,Q,R,S,E) [X,L,G,report] = dare(A,B,Q,...,'report') [X1,X2,L,report] = dare(A,B,Q,...,'implicit')
詳細
[X,L,G,rr] = dare(A,B,Q,R)
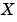 を計算します。
を計算します。
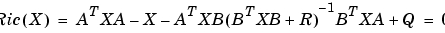
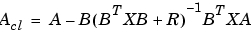
は、そのすべての固有値を単位円の内部にもっています。行列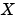 は、対称で、
は、対称で、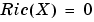 の安定化解と呼ばれます。また、
の安定化解と呼ばれます。また、[X,L,G,rr] = dare(A,B,Q,R)は、つぎのものが出力されます。
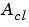 の固有値
の固有値L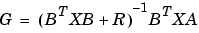
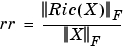
[X,L,G,rr] = dare(A,B,Q,R,S,E)
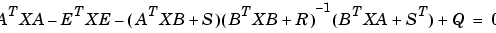
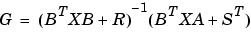
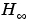 最適制御設計などのアプリケーションの開発を支援するために、2つのオプションが用意されています。
最適制御設計などのアプリケーションの開発を支援するために、2つのオプションが用意されています。
[X,L,G,report] = dare(A,B,Q,...,'report')は、解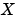 が存在しない場合、エラーメッセージを消去し、代わりに処理結果に対する情報
が存在しない場合、エラーメッセージを消去し、代わりに処理結果に対する情報reportを出力します。reportの値は、つぎの意味を表します。
-1 (失敗) 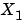 の
の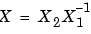 が、正則でない場合は、
が、正則でない場合は、-2 (失敗)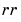 (成功)
(成功) また、 [X1,X2,L,report] = dare(A,B,Q,...,'implicit')も、エラーメッセージを消去しますが、この場合には、つぎのように陰的な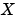 を出力します。
を出力します。
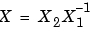
このオプションは、成功時にreport = 0を出力します。
アルゴリズム
dareは、[1]に示すアルゴリズムを実行します。QZアルゴリズムを使って、拡張したシンプレクティックペンシルを縮小し、その安定した不変部分空間を計算します。
制限
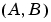 の組み合わせは、安定化可能でなければなりません(すなわち、単位円の外部のすべての
の組み合わせは、安定化可能でなければなりません(すなわち、単位円の外部のすべての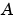 の固有値は、可制御でなければなりません)。さらに、関連したシンプレクティックペンシルは、単位円上に固有値をもつことはできません。この状態を維持するための十分条件は、
の固有値は、可制御でなければなりません)。さらに、関連したシンプレクティックペンシルは、単位円上に固有値をもつことはできません。この状態を維持するための十分条件は、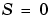 、かつ、
、かつ、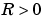 の場合、あるいは
の場合、あるいは
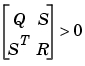
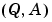 が検出可能であるということです。
が検出可能であるということです。
参考
care 連続時間Riccati方程式の解
dlyap 離散時間Lyapunov方程式の解
参考文献
[1] Arnold, W.F., III and A.J. Laub, "Generalized Eigenproblem Algorithms and Software for Algebraic Riccati Equations," Proc. IEEE, 72 (1984), pp. 1746-1754.
 | damp | dcgain |  |