| Control System Toolbox関数リファレンス | |
表示
[kest,L,P] = kalman(sys,Qn,Rn,Nn) [kest,L,P,M,Z] = kalman(sys,Qn,Rn,Nn) % 離散時間のみ [kest,L,P] = kalman(sys,Qn,Rn,Nn,sensors,known)
詳細
kalman
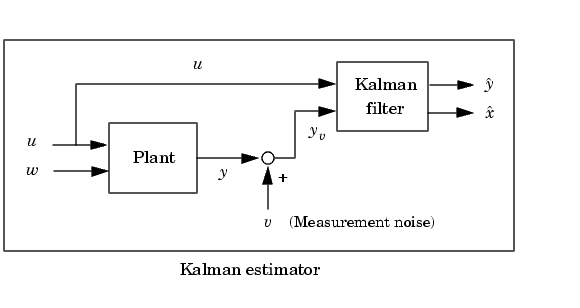
は、プラントの状態空間モデルおよびプロセス、測定ノイズ共分散データを与えて、Kalman状態推定器を設計します。Kalman推定器は、つぎの連続系または離散系推定問題に対する最適解です。
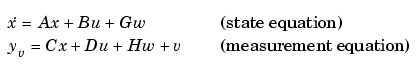
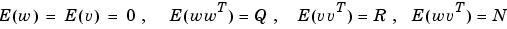
を満足するものとします。この連続プラントは、定常状態偏差の共分散
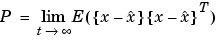
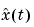を作成します。
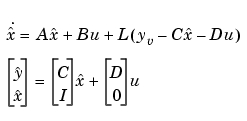
をもつKalmanフィルタです。この場合、フィルタゲイン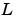
は、代数Riccati方程式を解くことによって決定されます。この推定器は、既知の入力
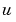と観測値
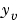を使って、出力推定
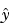および状態推定
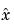を作成します。
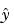は、真のプラント出力
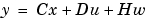
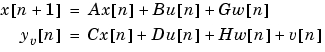
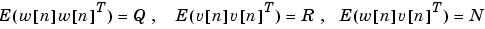
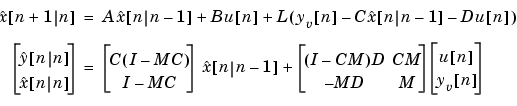
をもち、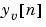
を含む利用可能なすべての観測値を使って、最適の"現在の"出力
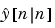および、状態推定値
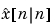を作成します。ゲイン行列
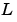および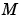
は、離散系Riccati方程式を解くことによって導かれます。イノベーションゲイン
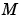は、つぎの新しい観測値
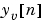を使って、予測値
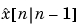を更新するために使用します。
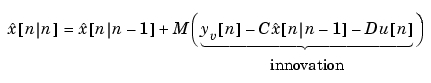
使用方法
[kest,L,P] = kalman(sys,Qn,Rn,Nn)は、プラントモデルsysおよびノイズ共分散データQn、Rn、Nn(上の行列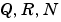
)が与えられた場合、Kalman推定器の状態空間モデルkestを出力します。sysは、行列をもつ状態空間モデルでなければなりません。
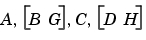
結果として得られる推定器kestは、入力として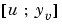
、および出力(あるいは、それらの離散系の相当値)として
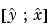をもっています。
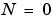の場合、最後の引数Nnは省略できます。
関数kalmanは、連続系、離散系いずれの問題も取り扱い、sysが連続系であれば連続系推定器を作成し、他の場合、離散系推定器を作成します。連続系では、kalmanは、KalmanゲインLと定常状態偏差の共分散行列Pも出力します。Pは、関連するRiccati方程式の解であることに注意してください。離散系では構文
[kest,L,P,M,Z] = kalman(sys,Qn,Rn,Nn)
は、フィルタゲイン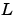
とイノベーションゲイン
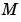および定常状態偏差の共分散
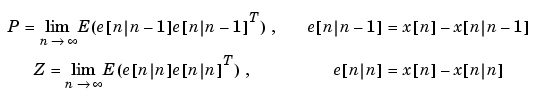
を出力します。 最終的に、より一般的なプラントsysに対して、構文
[kest,L,P] = kalman(sys,Qn,Rn,Nn,sensors,known) [kest,L,P,M,Z] = kalman(sys,Qn,Rn,Nn,sensors,known)
を用います。この場合は、既知の入力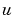
と確率的入力
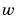が混在し、すべての出力が観測されるわけではありません。その時点で、既知のインデックスベクトルsensorsとknownは、sysのどの出力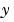
が観測され、どの入力
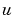が既知であるかを設定します。他のすべての入力は、確率的であると見なされます。
例題
マニュアルの"制御設計ツール"、"x-軸に対するLQG設計"、"カルマンフィルタ"を参照してください。
制限
プラントおよびノイズデータは、以下を満足する必要があります。
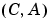は検出可能 
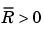と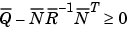 
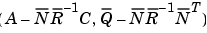は、虚軸上に非可制御モードをもっていません。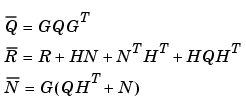 
参考
care
dare
estim
kalmd
lqgreg
lqr
参考文献
[1] Franklin, G.F., J.D. Powell, and M.L. Workman, Digital Control of Dynamic Systems, Second Edition, Addison-Wesley, 1990.
| | issiso | kalmd | |
とプロセスノイズ、測定白色ノイズ
は、