lqgreg (Control System Toolbox関数リファレンス)

状態フィードバックゲインとKalman推定器を与えて、LQGレギュレータを作成

表示

rlqg = lqgreg(kest,k)
rlqg = lqgreg(kest,k,'current')    % 離散時間のみ

rlqg = lqgreg(kest,k,controls)

詳細

lqgreg は、kalmanで設計したKalman推定器とlqr、dlqr、またはlqryのいずれかで設計した最適状態フィードバックゲインを結合することによって、LQGレギュレータを作成します。LQGレギュレータは、レギュレーション性能と制御効果との間の調整を行う2次型のコスト関数を最小にします。このレギュレータは、ダイナミックで、ノイズの多い出力測定値に応じて調整指令を作成します。

連続系では、LQG レギュレータが、制御入力

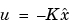
を作成します。ここで、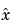はKalman状態推定値です。レギュレータの状態空間方程式は、つぎのようになります。

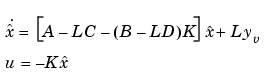
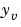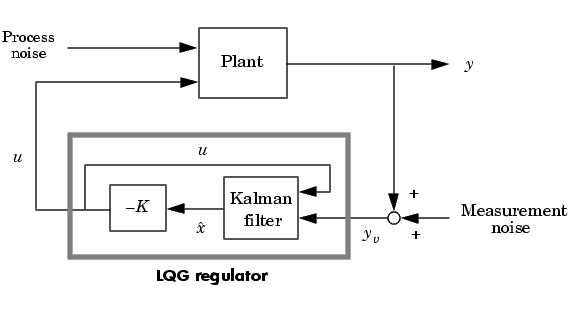
ここで、は、プラント出力測定値のベクトルです(背景および表記については、kalmanを参照してください)。つぎの図は、プラントに関するこのダイナミックレギュレータを示しています。

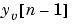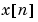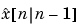離散系では、までの観測値に基づくの予測値か、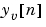を含むすべての利用可能な測定値に基づく現在の状態推定値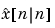のどちらかを使って、LQGレギュレータを作成することができます。レギュレータ

は、常に明確に定義されていますが、現在のレギュレータ

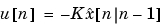
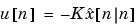
は、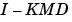が可逆である場合にのみ因果性をもちます(表記については、kalmanを参照)。さらに、現在のレギュレータの具体的実現は、観測値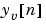が一度利用できると、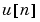を計算するための処理時間が必要になります(これは、フィードバックループの中のむだ時間となります)。

使用方法

rlqg = lqgreg(kest,k) は、Kalman推定器kestおよび状態フィードバックゲイン行列kを与えて、LQGレギュレータrlqg(状態空間モデ)を出力します。同じ関数が、連続系と離散系の両方のケースを扱います。 kestとkの設計には、以下のように矛盾がないようにします。

連続系プラント用連続レギュレータ： lqrまたはlqryおよびkalmanを使用

離散系プラント用離散レギュレータ： dlqrまたはlqryおよびkalmanを使用

連続系プラント用離散レギュレータ： lqrdおよびkalmdを使用

離散系では、lqgregは、デフォルトでレギュレータ

を作成します("詳細"を参照)。代わりに現在のLQGレギュレータ

を作成するためには、つぎの構文を使います。

rlqg = lqgreg(kest,k,'current')

この構文は、離散系問題に対してのみ意味があります。

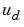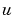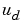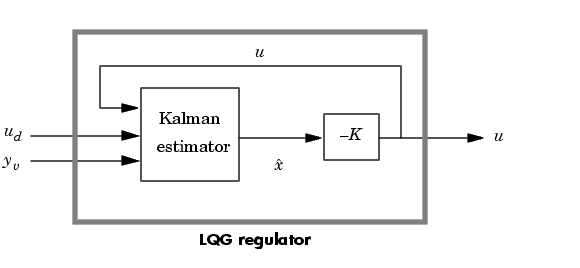
rlqg = lqgreg(kest,k,controls)は、付加的な既知プラント入力にアクセスする推定器を取り扱います。インデックスベクトルcontrolsは、どの推定器入力が制御であるかを設定し、結果として得られるLQGレギュレータrlqgは、入力として、と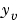をもっています(つぎの図を参照)。

注意: LQGレギュレータは、必ず正のフィードバックを使ってプラントに結合してください。

例題

"LQGレギュレータ"を参照してください。

参考
kalman Kalman推定器の設計

kalmd 連続系プラントに対する離散Kalman推定器

lqr, dlqr 状態フィードバックLQレギュレータ

lqrd 連続系プラントに対する離散LQレギュレータ

lqry 重み付き出力をもつレギュレータ

reg 状態フィードバックゲインと推定器ゲインを与え、レギュレータを作成ゲイン

lft lqr