| Control System Toolbox関数リファレンス | |
表示
[X,L,G,rr] = care(A,B,Q) [X,L,G,rr] = care(A,B,Q,R,S,E) [X,L,G,report] = care(A,B,Q,...,'report') [X1,X2,L,report] = care(A,B,Q,...,'implicit')
詳細
[X,L,G,rr] = care(A,B,Q) は、つぎの代数Riccati方程式の一意的な解を計算します。
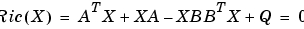
ここで、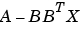
は、開左半平面にすべての固有値をもっていなければなりません。行列
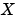は対称で、
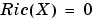の安定化解と呼ばれます。また 、[X,L,G,rr] = care(A,B,Q)は、つぎのものを出力します。
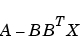の固有値L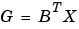
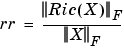
[X,L,G,rr] = care(A,B,Q,R,S,E)では、つぎの一般的なRiccati方程式を解きます。
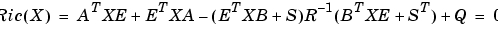
ここで、ゲイン行列は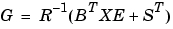
であり、"閉ループ"固有値は、L = eig(A-B*G,E)です。
最適制御設計などのアプリケーションの開発を支援するために、2つのオプションが用意されています。
[X,L,G,report] = care(A,B,Q,...,'report')は、解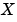
が存在しない場合、エラーメッセージを消去し、代わりに処理結果に対する情報をreportに出力します。
-1 (失敗)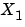 
の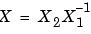
が正則でない場合は、-2 (失敗) 
(成功) また、 [X1,X2,L,report] = care(A,B,Q,...,'implicit') も、エラーメッセージを消去しますが、つぎのように陰的な型で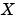
を出力します。
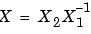
このオプションは、成功した場合、report=0を出力することに注意してください。
例題 1
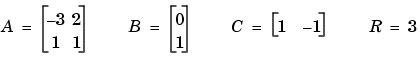
a = [-3 2;1 1] b = [0 ; 1] c = [1 -1] r = 3 [x,l,g] = care(a,b,c'*c,r)
x
x =
0.5895 1.8216
1.8216 8.8188
aおよびa-b*gの固有値を比較すれば、この解が実際に安定であることが確認できます。
[eig(a) eig(a-b*g)]
ans =
-3.4495 -3.5026
1.4495 -1.4370
最後に、閉ループ固有値eig(a-b*g)は、出力変数lと一致します。
l l = -3.5026 -1.4370
例題 2
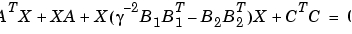
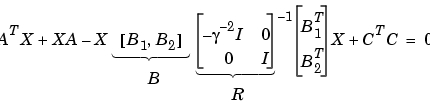
ここで、つぎのように安定化された解
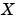を計算することができます。
B = [B1 , B2] m1 = size(B1,2) m2 = size(B2,2) R = [-g^2*eye(m1) zeros(m1,m2) ; zeros(m2,m1) eye(m2)] X = care(A,B,C'*C,R)
アルゴリズム
careは、[1]で説明したアルゴリズムを実現します。careは、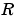
の条件数が良く、かつ
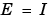である場合に、Hamilton行列と共に機能し、その他の場合、拡張Hamiltonペンシルを用い、QZアルゴリズムを使用します。
制限
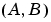の組み合わせは、安定化可能でなければなりません(すなわち、すべての不安定なモードは可制御です)。また、関連するHamilton行列またはHamiltonペンシルは、虚軸上に固有値をもつことはできません。この状態を維持するための十分条件は、
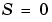かつ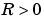
の場合、または、
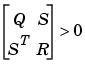の場合、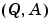
が検出可能であるということです。
参考
dare 離散系Riccati方程式の解
lyap 連続時間Lyapunov方程式の解
参考文献
[1] Arnold, W.F., III and A.J. Laub, "Generalized Eigenproblem Algorithms and Software for Algebraic Riccati Equations," Proc. IEEE, 72 (1984),
pp. 1746-1754.
| | canon | chgunits | |
様式のRiccati方程式