

| Control System Toolbox関数リファレンス |   |
表示
[Kd,S,e] = lqrd(A,B,Q,R,Ts) [Kd,S,e] = lqrd(A,B,Q,R,N,Ts)
詳細
lqrd
は、lqrを使って設計された連続系状態フィードバックレギュレータに類似した応答特性をもつ離散系全状態フィードバックレギュレータを設計します。このコマンドは、連続系状態フィードバックゲインの設計に成功した後、ディジタル化のためのゲイン行列を設計するのに利用できます。
[Kd,S,e] = lqrd(A,B,Q,R,Ts)
は、連続系コスト関数
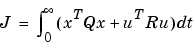
と等価の離散系コスト関数を最小化して、離散系状態フィードバック則
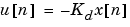
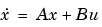
を設定します。そして、Tsは、離散系レギュレータのサンプル時間を設定します。また、離散化した問題に対する離散Riccati方程式の解Sと離散閉ループ固有値 e = eig(Ad-Bd*Kd)も出力します。
[Kd,S,e] = lqrd(A,B,Q,R,N,Ts)
は、コスト関数
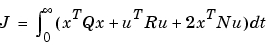
アルゴリズム
等価な離散系ゲイン行列Kdは、サンプル時間Tsとゼロ次ホールド近似を使って、連続系プラントを離散化したり、行列の重みを付けることによって求まります。
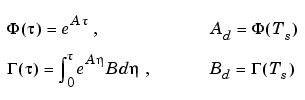
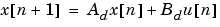
をもち、等価な離散系コスト関数に対する重み行列は、つぎのようになります。
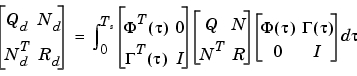
積分は、Van Loanによる行列指数の公式([2を参照)を使って計算されます。プラントは、c2dを使って離散化され、ゲイン行列はdlqrを使って離散化したデータから計算されます。
制限
離散化問題データは、dlqrに対する必要条件を満たさなければなりません。
参考
c2d
dlqr
kalmd
lqr
参考文献
[1] Franklin, G.F., J.D. Powell, and M.L. Workman, Digital Control of Dynamic Systems, Second Edition, Addison-Wesley, 1980, pp. 439-440
[2] Van Loan, C.F., "Computing Integrals Involving the Matrix Exponential," IEEE Trans. Automatic Control, AC-15, October 1970.
 | lqr | lqry |  |