| Getting Started |
時間応答と周波数応答
時間応答は、入力や外乱の特殊なクラスに対して、線形モデルの時間領域での過渡的振る舞いを調べます。ユーザは、時間応答から、立ち上がり時間、整定時間、オーバシュート、定常偏差のようなシステムの特性を決定することができます。Control
System Toolboxは、Step応答、Impulse応答、初期値応答、一般的な線形シミュレーション用の関数を用意しています。関数lsimとrandn(ランダム入力ベクトルを作成するために、Using
MATLABを参照)を使って、白色ノイズ入力の応答をシミュレーションできます。
時間応答コマンドに加えて、Control System Toolboxは、周波数応答プロット用のコマンドも提供しています。これらのコマンドを使って、つぎの図を作成できます。
加えて、関数marginは、与えられたSISO開ループモデルに対して、ゲイン余裕と位相余裕を決定します。これらの関数は、単一の線形モデルまたはLTI配列にも適用できます。
つぎのテーブルは、利用可能な時間応答関数と周波数応答関数の名前と内容です。
| コマンド |
詳細 |
|
Bode線図の計算 |
|
単一複素周波数で、周波数応答を計算(FRDモデル用ではありません) |
|
周波数群に対する周波数応答を計算 |
|
入力信号発生器(関数lsim用) |
|
Impulse応答 |
|
初期値応答 |
|
任意の入力に対する応答のシミュレーション |
|
ゲイン余裕と位相余裕の計算 |
|
Nichols線図上にグリッドを作成 |
|
Nichols線図の計算 |
|
Nyquist線図の計算 |
|
極-零点図の計算 |
|
Step応答 |
関数step,impulse,initialは、時間応答プロット用に適切なシミュレーション平面を自動的に作成します。このシンタックスは、つぎのようになります。
step(modelname) impulse(modelname) initial(modelname,x0) % x0 = 初期状態ベクトル
ここで、modelnameは、連続または離散のLTIモデルまたはLTI配列です。
例題:MIMOモデル応答のプロット
MIMOモデルに対して、時間応答や周波数応答のコマンドは、I/Oチャンネル毎に一つの図をもつプロットの配列を作成します。たとえば、
h = [tf(10,[1 2 10]) , tf(1,[1 1])] step(h)
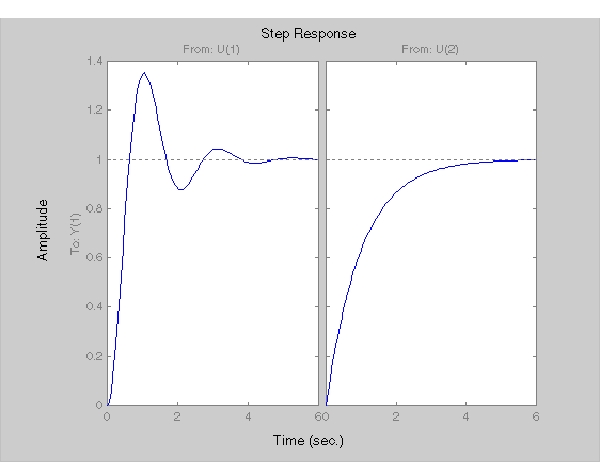
シミュレーションの時間軸は、モデルのダイナミクスをベースに自動的に決定されます。シミュレーションの最終時間を設定することにより、この自動モードを無効にできます。
step(system,10) % 0秒から10秒をシミュレートする
または、等間隔の時間サンプルのベクトルを設定することによっても無効にできます。
t = 0:0.01:10 % 0.01秒間隔の時間サンプルベクトル step(system,t)
bode(modelname) nichols(modelname) nyquist(modelname) sigma(model_name)
は、連続モデルと離散モデルを共に扱えます。これらのコマンドは、SISO線形モデルの周波数応答図を作成します。また、MIMOの場合は、プロット配列を作成します。応答を計算するために使用する周波数グリッドは、システムの極や零点をベースに自動的に選択されます。
| 時間応答と周波数応答用のコマンド | マルチシステムのプロットと比較 |