bode (Control System Toolbox関数リファレンス)

LTIモデルのBode周波数応答の計算

表示

bode(sys)
bode(sys,w)

bode(sys1,sys2,...,sysN)
bode(sys1,sys2,...,sysN,w)
bode(sys1,'PlotStyle1',...,sysN,'PlotStyleN')

[mag,phase,w] = bode(sys)

詳細

bodeは、LTIシステムの周波数応答のゲインと位相を計算します。左辺の出力引数を設定しない場合、bodeはスクリーン上にBode線図を表示します。ゲインはデシベル(dB)、位相は度単位でプロットされます。magのデシベル計算は、20*log10(abs(frsys))で実行されます。ここで、frsysは、sysの周波数応答です。Bode線図は、ゲイン余裕、位相余裕、DCゲイン、帯域幅、外乱抑制、安定性などのシステムの特性を解析するために使用します。

bode(sys)は、任意のLTIモデルsysのBode応答をプロットします。このモデルは、連続系、離散系のいずれでも、あるいは、SISO、MIMOのいずれでも可能です。MIMOの場合、bodeは、Bode線図の配列を作成し、各々のプロットは、特定の入出力チャンネルに関するBode線図を表示します。周波数範囲は、システム極および零点を基に自動的に決定されます。

bode(sys,w)は、プロットに使用する周波数範囲または周波数点を明示的に設定します。特定の周波数区間[wmin,wmax]上で計算するには、w = {wmin,wmax}を設定します。特定の周波数点を使用するには、wを希望する周波数ベクトルで設定します。logspaceを使って、対数的に等間隔な周波数ベクトルを作成することもできます。すべての周波数は、ラジアン/秒単位で設定します。

bode(sys1,sys2,...,sysN)、または、 bode(sys1,sys2,...,sysN,w)は、1つのFigure上に複数のLTIモデルのBode応答をプロットします。すべてのシステムは、同数の入力と出力をもたなければなりませんが、それ以外については、連続系と離散系が混在することも可能です。この構文は、複数システムのBode応答を比較するときに役立ちます。

bode(sys1,'PlotStyle1',...,sysN,'PlotStyleN')は、さらに各システムをプロットするのに、どのカラーやラインスタイル、マーカを使用するのかを設定します。たとえば、

bode(sys1,'r--',sys2,'gx')

は、最初のシステムsys1に対して赤の破線を用い、2番目のシステムsys2に対して緑の'x'マーカを用います。

つぎのように左辺の引数を設定すると、

[mag,phase,w] = bode(sys)
[mag,phase] = bode(sys,w)

周波数w(ラジアン/秒)で、周波数応答のゲインと位相(度)を出力します。出力magおよびphaseは、周波数を最後の次元とする3次元配列になります(詳細については、"引数"を参照してください)。求まるゲインは、次式を使って、デシベルに変換できます。

magdb = 20*log10(mag)

注意事項

sysがFRDモデルbode(sys,w)で表現されている場合、wはsys.frequencyの中にのみ周波数を含みます。

引数

出力引数magおよびphaseは、つぎの次元をもつ 3次元配列です。

(出力数)x(入力数)x(wの長さ)

SISOシステムの場合、mag(1,1,k)およびphase(1,1,k)は、周波数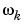= w(k)での応答のゲインと位相を与えます。

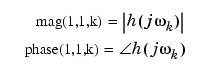
MIMOシステムは、SISOシステムの配列として取り扱われ、ゲインと位相は、各SISO成分h_ijに対して、別々に計算されます(h_ijは、入力jから出力iへの伝達関数です)。そして、値mag(i,j,k) およびphase(i,j,k)は、周波数w(k)でのh_ijの応答特性です。

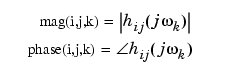
例題

連続SISOシステム

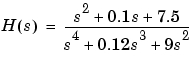
のBode応答を、つぎのようにしてプロットすることができます。

g = tf([1 0.1 7.5],[1 0.12 9 0 0]);
bode(g)

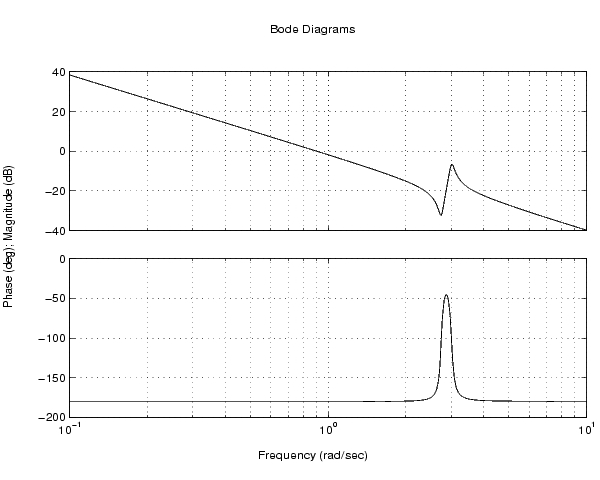
たとえば、0.1から100ラジアン/秒のように、より広い周波数範囲での応答をプロットするには、つぎのように入力します。

bode(g,{0.1 , 100})

サンプル時間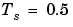秒とゼロ次ホールドを使って、このシステムを離散化し、連続系と離散系の応答を比較してみましょう。

gd = c2d(g,0.5)
bode(g,'r',gd,'b--')

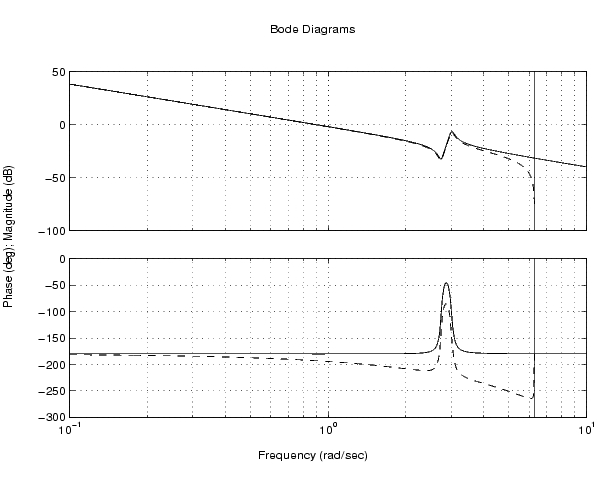
アルゴリズム

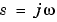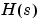連続系の場合、関数bodeは虚軸上で伝達関数を計算することにより、周波数応答を計算します。正の周波数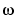のみを対象にします。状態空間モデルの場合、周波数応答は、つぎのようになります。

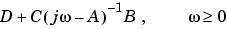
数値的に安全な場合、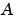を対角化して、高速処理を行ないます。そうでない場合、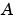は、上Hessenberg形式に変換して、この変換された構造を利用して、線形方程式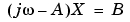が、各周波数点で計算されます。Hessenberg形式への変換は、効率と信頼性とのバランスを保ちます。この技法に関する詳細については、[1]を参照してください。

離散系の場合、周波数応答は単位円上で伝達関数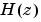を計算することによって算出されます。解釈の便宜上、単位円の上半分をつぎのようにパラメータ化します。

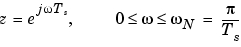
ここで、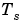はサンプル時間で、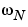はナイキスト周波数と呼ばれます。等価な連続系周波数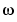は、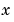-軸の変数として使用されます。

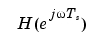
は、周期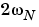の周期関数であるので、bodeは、ナイキスト周波数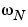までしか応答をプロットしません。サンプル時間を設定しない場合は、デフォルト値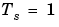が設定されます。

診断

システムが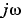軸(または離散系の場合、単位円)上に極をもつ場合、または、wが、この周波数点を含む場合、ゲインは無限大で、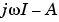は特異値になり、bodeは、つぎのワーニングメッセージを出力します。

Singularity in freq. response due to jw-axis or unit circle pole.

参考
evalfr 単一複素数周波数点での応答

freqresp 周波数応答計算

ltiview LTIシステムビューワの起動

nichols Nichols 線図

nyquist Nyquist 線図

sigma 特異値プロット

参考文献

[1] Laub, A.J., "Efficient Multivariable Frequency Response Computations," IEEE Transactions on Automatic Control, AC-26 (1981), pp. 407-408.

balreal c2d