freqresp (Control System Toolbox関数リファレンス)

周波数のグリッドに対して周波数応答を計算

表示

H = freqresp(sys,w)

詳細

H = freqresp(sys,w) は、ベクトルwで設定した実周波数点でのLTIモデルsysの周波数応答を計算します。周波数の単位は、ラジアン/秒でなければなりません。単一のLTIモデルに対して、freqresp(sys,w)は、最後の次元に周波数を設定した3次元配列Hを出力します。また、サイズ[Ny Nu S1 ... Sn]のLTI配列に対して、freqresp(sys,w)は、[Ny-Nu-S1-...-Sn]の長さの配列を出力します。

連続系の場合、周波数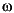での応答は、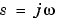での伝達関数値です。状態空間モデルの場合、この値は、

で与えられます。

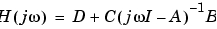
離散系の場合、実周波数w(1),..., w(N)は、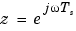変換を使って単位円上の点に射影されます。この場合、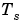はサンプル時間です。つぎに、伝達関数は、結果として得られる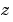の値で計算されます。サンプル時間が設定されていないモデルでは、デフォルトの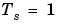が使用されます。

注意事項

sysがFRDモデルfreqresp(sys,w)の場合、wは、sys.frequencyに周波数のみを含みます。

引数

出力引数Hは、つぎの次元をもつ 3-次元配列です。

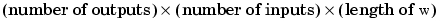
SISOシステムの場合、H(1,1,k)は周波数w(k)でのスカラ応答を与えます。MIMOシステムの場合、w(k)での周波数応答は、出力と同数の行と入力と同数の列をもつ行列H(:,:,k)です。

例題

つぎの行列

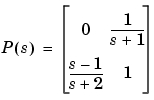
の周波数応答を、周波数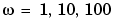について計算します。つぎのように入力します。

w = [1 10 100]
H = freqresp(P,w)
H(:,:,1) =
 
        0            0.5000- 0.5000i
  -0.2000+ 0.6000i   1.0000         
 
 
H(:,:,2) =
 
        0            0.0099- 0.0990i
   0.9423+ 0.2885i   1.0000         
 
 
H(:,:,3) =
 
        0            0.0001- 0.0100i
   0.9994+ 0.0300i   1.0000

表示されている3つの行列は、に対するの値です。

3次元配列Hの中の3番目のインデックスは、周波数ベクトルwに対応するので、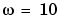ラジアン/秒での周波数応答は、つぎのようにして取り出すことができます。

H(:,:,w==10)

ans =
        0            0.0099- 0.0990i
   0.9423+ 0.2885i   1.0000

アルゴリズム

伝達関数または零点-極-ゲインモデルの場合、freqrespは設定した周波数点での分子と分母を計算します。連続系状態空間モデルの場合、周波数応答は、つぎのようになります。

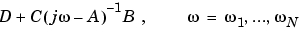
数値的に安全な場合、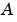はこの式を迅速に計算するために周波数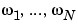で対角化されます。それ以外の場合、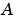は上Hessenberg型に変換され、線形方程式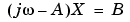は、Hessenberg構造を利用して各周波数点で解かれます。Hessenberg型に変換すると、効率と信頼性との間の適切な均衡が保たれます。この技法に関する詳細については、[1]を参照してください。

診断

システムが、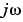軸(または離散系の場合は単位円)上に極をもち、wがこの周波数点を含む場合、ゲインは無限で、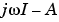は特異行列となり、freqrespは、つぎのワーニングメッセージを出します。

Singularity in freq. response due to jw-axis or unit circle pole.

参考
evalfr 単一複素数周波数点での応答

bode Bode線図

nyquist Nyquist 線図

nichols Nichols 線図

sigma 特異値プロット

ltiview LTIシステムビューワの起動

参考文献

[1] Laub, A.J., "Efficient Multivariable Frequency Response Computations," IEEE Transactions on Automatic Control, AC-26 (1981), pp. 407-408.

frdata gensig