| Control System Toolbox関数リファレンス | |
表示
lsim(sys,u,t) lsim(sys,u,t,x0) lsim(sys1,sys2,...,sysN,u,t) lsim(sys1,sys2,...,sysN,u,t,x0) lsim(sys1,'PlotStyle1',...,sysN,'PlotStyleN',u,t) [y,t,x] = lsim(sys,u,t,x0)
詳細
lsim
は、任意の入力に対する連続時間または離散時間線形システムの(時間)応答をシミュレーションします。左辺の引数を設定しないと、lsimはスクリーン上に応答をプロットします。
lsim(sys,u,t)
は、入力uとその各要素の時刻tに対するLTI モデルsysの時間応答図を作成します。ベクトルtは、シミュレーションに対する時間サンプルを設定し、つぎの定間隔をもつサンプルから構成されています。
t = 0:dt:Tfinal
行列uは、時間サンプル(length(t))と同数の行数とシステム入力と同数の列数をもっていなければなりません。各行u(i,:)は、時間サンプルt(i)での入力値を設定します。
LTIモデルsysは、連続系でも離散系でも、また、SISOでも、MIMOでも構いません。離散系では、uはシステムと同じ間隔でサンプリングしなければなりません(その場合、tは余分なので、省略するか、空行列に設定します)。連続系では、連続系モデルを離散化するために、時間サンプリング dt=t(2)-t(1) を使用します。dtが大き過ぎて(アンダーサンプリング)、実際生じる振動が現われなくなる可能性がある場合には、自動的にリサンプリングが実行されます(下の"アルゴリズム"を参照してください)。
lsim(sys,u,t,x0)
は、さらに、システムの状態に対する初期値x0を設定します。この構文は、状態空間モデルのみに適用されます。
lsim(sys1,sys2,...,sysN,u,t)
は、同じ入力時刻歴t、uに対する複数のLTIモデルの応答をシミュレーションし、1つのFigureの中にこれらの応答をプロットします。bode、または 、plotと同様に、システム毎に特定のカラー、ラインスタイル、マーカを設定することができます。たとえば、つぎのとおりです。
lsim(sys1,'y:',sys2,'g--',u,t,x0)
マルチシステムの挙動は、bodeまたはstepの挙動と同様です。
[y,t] = lsim(sys,u,t) [y,t,x] = lsim(sys,u,t) % 状態空間モデルに対してのみ [y,t,x] = lsim(sys,u,t,x0) % 初期条件付き
は、出力応答yとシミュレーションに使用する時間ベクトルt、状態量の時間変化x(状態空間モデルに対してのみ)を出力し、スクリーン上にはプロットされません。行列yは、時間サンプル(length(t))と同数の行数とシステム出力と同数の列数をもっています。同じことは、出力を状態に置き換えた行列xについても言えます。入力データのサンプリング間隔が短い場合、出力tは設定した時間ベクトルと異なる場合があります(下の"アルゴリズム"を参照)。
例題
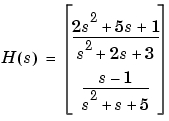
の応答を4秒の周期をもつ矩形波に対して、シミュレーションしプロットします。まず、gensigで、矩形波を作成します。サンプリングは、0.1秒間隔で 10秒間行います。
[u,t] = gensig('square',4,10,0.1)
H = [tf([2 5 1],[1 2 3]) ; tf([1 -1],[1 1 5])] lsim(H,u,t)
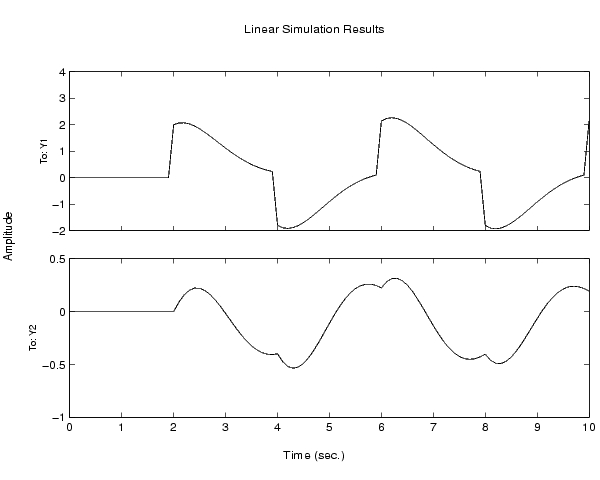
アルゴリズム
離散システムは、ltitr(状態空間)、または、filter(伝達関数および零点-極-ゲイン)を使ってシミュレーションします。
連続システムは、'zoh'または'foh'のいずれかの方法を使って、c2dで離散化します('foh'はスムーズな入力信号に使用し、'zoh'はパルス波や矩形波などの不連続信号に使用します)。デフォルトでは、サンプリング周期はユーザ設定の時間サンプルtの間隔dtに設定されます。ただし、dtがサンプル間の挙動を取り込めるだけ小さな値でない場合、lsimは、より小さなサンプリング周期を選択し、スムーズな信号に対しては線形補間を用い、矩形波信号に対してはゼロ次ホールドを使って入力データをリサンプリングします。この場合、lsimが出力する時間ベクトルは、設定したtベクトルとは異なります。
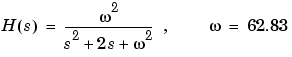
を考えます。周期1秒の矩形波に対するその応答をシミュレーションするために、つぎのように処理することができます。
w2 = 62.83^2 h = tf(w2,[1 2 w2]) t = 0:0.1:5; % 時間サンプルのベクトル u = (rem(t,1)>=0.5); % 矩形波の値 lsim(h,u,t)
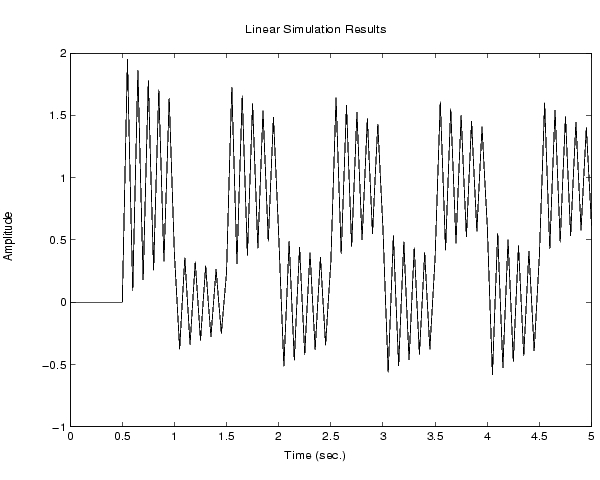
応答は、強い振動を示します。lsimは、振動状態を表すために入力をリサンプルしているということを、このプロットからはわかりません。これを見るためには、サンプリング周期0.1秒(tベクトルでの間隔)を使って、を離散化し、離散化モデルの応答をシミュレーションします。
hd = c2d(h,0.1) lsim(hd,u,t)
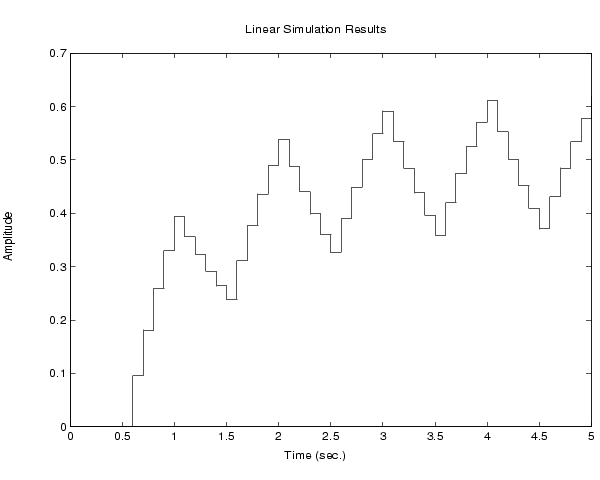
2つの応答は、かなり違っているように見えます。この違いを明確にするために、
lsim(h,'b--',hd,'r-',u,t)
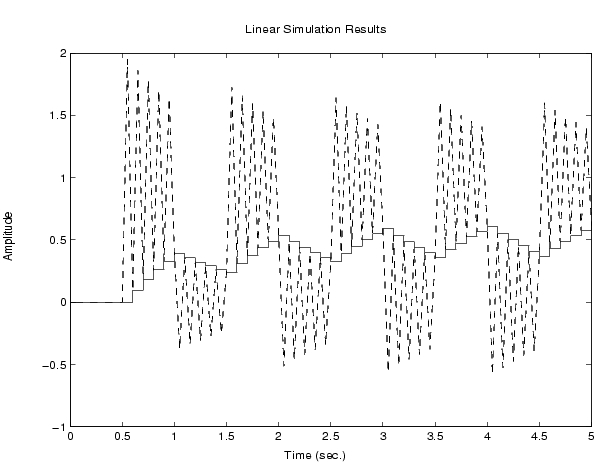
原因は明らかです。hdのサンプリング間隔が粗く、その応答(実線)は連続モデル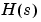
のサンプル間の振動を隠しています。
仮定したサンプリングdt=t(2)-t(1) とシステムダイナミックスとを比較することにより、lsimは、そのような不十分なサンプリング間隔を検出し、正確な連続時間シミュレーションを行うように入力をリサンプリングします。
参考
gensig lsim
コマンドに対する入力信号の発生
impulse
initial
ltiview LTIシステムビューワの起動
step
| | lqry | ltiview | |