remez (Signal Processing Toolbox)

Parks-McClellan最適FIRフィルタの設計

表示

b = remez(n,f,a)
b = remez(n,f,a,w)
b = remez(n,f,a,'ftype')
b = remez(n,f,a,w,'ftype')
b = remez(...,{lgrid})
b = remez(n,f,'fresp',w)
b = remez(n,f,'fresp',w,'ftype')
b = remez(n,f,{'fresp',p1,p2,...},w)
b = remez(n,f,{'fresp',p1,p2,...},w,'ftype')
[b,delta] = remez(...)
[b,delta,opt] = remez(...)

詳細

remezは、Parks-McClellanアルゴリズム(参考文献[1])を使って、線形位相FIRフィルタを設計します。Parks-McClellanアルゴリズムは、Remez交換アルゴリズムとChebyshev 近似理論を使って、希望の周波数応答と実際の周波数応答との最適近似をもつフィルタを設計します。設計されるフィルタは、希望する周波数応答と実際の周波数応答との間の最大誤差が最小化されるという意味で最適です。この方法で設計されたフィルタは、その周波数応答において等リップルの挙動を示すため、等リップルフィルタと呼ばれることもあります。

b = remez(n,f,a) は、ベクトルfとaで与えられた周波数応答特性とできるだけ一致する(n+1)個の係数を含む行ベクトルbを出力します。

bに出力されるフィルタ係数(タップ)は、つぎの対称性をもっています。

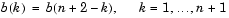
ベクトル fおよびaは、フィルタの周波数-ゲイン特性を設定します。

fは、0から1の範囲で設定される正規化された周波数点のベクトルで、1はサンプリング周波数の1/2(Nyquist周波数)に相当します。周波数は、昇順でなければなりません。

aは、fに設定した点での希望するゲイン応答ベクトルです。

kが奇数の場合、点(f(k), f(k+1))の間の周波数での希望の振幅は、点(f(k), a(k)) と点(f(k+1), a(k+1))を直線で結んだものです。

kが偶数の場合、点(f(k), f(k+1))の間の周波数での希望の振幅は、特に設定されません。そのような点の間は、遷移領域、すなわち、"配慮されない"領域です。

f と a は、同じ長さで、偶数でなければなりません。

希望の周波数応答を定義するベクトルfとaの関係は、つぎのようになります。

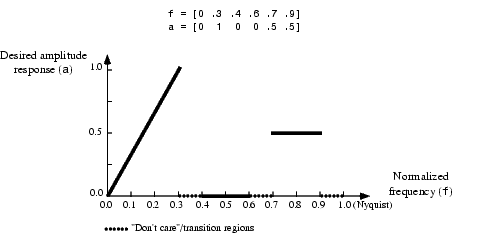
remez は、Nyquist 周波数で、通過帯域をもつ型にするために、偶数のフィルタ次数を使います。これは、奇数のフィルタ次数に対して、Nyquist 周波数での周波数応答は、必ず、0になるためです。n に奇数の値を設定すると、remez は、自動的に1を加えます。

remez(n,f,a,w) は、ベクトルwの重みを使って、各周波数帯域の近似に重みを付けます。wの長さは、fおよびaの長さの1/2で、1帯域毎に1つの重みを設定します。

b = remez(n,f,a,'ftype') 、および、

b = remez(n,f,a,w,'ftype') は、フィルタのタイプを設定します。

'hilbert'：奇数対称性をもつ線形位相フィルタ(III型、IV型)

bに出力される係数は、 b(k) = -b(n + 2 -k), k = 1,...,n + 1の関係をもっています。このクラスのフィルタは、帯域全体にわたり希望の振幅1をもつHilbert変換子を含んでいます。

たとえば、

h = remez(30,[0.1 0.9],[1 1],'hilbert');

は、長さ31の近似的FIR Hilbert変換子を設計します。

'differentiator'：特殊重み付け法を使ったIII型、IV型フィルタ

非ゼロ振幅帯域で誤差に1/f倍の重みが付けられ、それによって低周波数帯域での誤差は高周波数帯域での誤差よりはるかに小さくなります。周波数に比例する振幅特性をもつFIR微分器では、これらのフィルタは最大相対誤差(希望の振幅に対する誤差の比率の最大値)を最小化します。

b = remez(...,{lgrid}) は、周波数グリッドの密度をコントロールする整数lgridを使います。これは、大まかに、(lgrid*n)/(2*bw)の周波数点数になります。ここで、bwは、fによりカバーされる全周波数帯域[0,1]の中に含まれるものです。lgridを増加させると、より厳密な意味で等リップルになりますが、計算時間は増えます。デフォルト値は16で、lgridに対して設定できる最小値です。{lgrid}引数は、1行1列のセル配列です。

b = remez(n,f,'fresp',w) は、関数frespにより設定される応答を最適に近似する周波数-振幅特性をもつn次のFIRフィルタのn+1 個の係数を含む行ベクトルbを出力します。関数は、つぎの書式をもって、remezと共に読み込まれます。

[dh,dw] = fresp(n,f,gf,w)

引数は、remezのものと同じです。

nは、フィルタ次数です。

f は、0 と 1の間で単調関数になっている正規化した周波数帯域エッジを要素とするベクトルで、1はNyquist周波数です。

gfは、remezにより設定された周波数帯域で線形に内挿されます。gfは、応答を推定する周波数グリッドを決定します。そして、opt 構造のfgridメンバーにcremezにより出力された同じデータを含んでいます。

w は、最適化の間に使われる帯域毎の正の実数で定義した重みです。wは、remezを実行する場合、オプションです。設定していない場合、'fresp'に渡す前に単位大きさの重みを設定します。

dh と dw は、グリッドgfの中の各周波数で計算する希望する複素周波数応答と帯域に適用する重みです。

remezが読み込む前もって定義している周波数応答関数(fresp)は、signal/privateディレクトリのremezfrfです。

b = remez(n,f,{'fresp',p1,p2,...},w) は、frespに渡される付加的なパラメータ(p1, p2,等)を設定します。b = remez(n,f,a,w) は、 b = remez(n,f,{'remezfrf',a},w)と等価で、ここで、aはfで設定されている点で希望する振幅を含むベクトルです。

b = remez(n,f,'fresp',w,'ftype') および

b = remez(n,f,{'fresp',p1,p2,...},w,'ftype') は、対称(偶数)フィルタでなく非対称(奇数)フィルタを設計します。ここで、'ftype'は、微分器に対して'd' 、Hilbert変換子に対して'h' のどちらかを設定します。

ftypeに対する設定がない場合、前もってfrespの読み込みがなされ、デフォルトの対称性を示すsymが設定されます。つぎの書式を使います。

sym = fresp('defaults',{n,f,[],w,p1,p2,...})

引数 n, f, w等は、symへの適切な値を決めるために必ず使われるものです。これは、remezが'even'でも'odd'でも必要になります。fresp関数が、この読み込み書式でサポートされていなければ、remez はデフォルトの対称性を使います。

[b,delta] = remez(...) は、リップルの最大の大きさをdeltaに出力します。

[b,delta,opt] = remez(...) は、つぎのメンバーをもつオプションの計算結果を含む構造体optを出力します。

opt.fgrid
フィルタ設計の最適化に使用する周波数グリッドベクトル

opt.des
opt.fgrid の各点に対する希望する周波数応答

opt.wt
opt.fgridの中の各点に対する重み

opt.H
opt.fgridの中の各点に対する実際の周波数応答

opt.error
opt.fgrid の中の各点でのエラー(opt.des-opt.H)

opt.iextr
opt.fgridの中に余分な周波数に対するインデックスベクトル

opt.fextr
余分な周波数のベクトル

`opt.fgrid`	フィルタ設計の最適化に使用する周波数グリッドベクトル
`opt.des`	`opt.fgrid` の各点に対する希望する周波数応答
`opt.wt`	`opt.fgrid`の中の各点に対する重み
`opt.H`	`opt.fgrid`の中の各点に対する実際の周波数応答
`opt.error`	`opt.fgrid` の中の各点でのエラー(`opt.des-opt.H`)
`opt.iextr`	`opt.fgrid`の中に余分な周波数に対するインデックスベクトル
`opt.fextr`	余分な周波数のベクトル

例題

17次のParks-McClellan バンドパスフィルタの希望の周波数応答と実際の周波数応答をグラフ表示にします。

f = [0 0.3 0.4 0.6 0.7 1]; a = [0 0 1 1 0 0];
b = remez(17,f,a);
[h,w] = freqz(b,1,512);
plot(f,a,w/pi,abs(h))
legend('Ideal','remez Design')

アルゴリズム

remezは、参考文献[1]に記述されているFORTRANコードのMEXファイル型で、任意の数の線形帯域をもつ任意の長さのフィルタを設計するように変更したものです。

remezは、I 型、II 型、III 型、およびIV 型の線形位相フィルタを設計します。I 型とII 型は、それぞれnが偶数と奇数の場合のデフォルトですが、'hilbert'や'differentiator'フラグを付けるとIII 型(nが偶数の場合)やIV 型(nが奇数の場合)フィルタが作成されます。さまざまなフィルタのタイプは、それぞれ異なる対称性と周波数応答に関するいくつかの制約があります(詳細については、参考文献[5]を参照)。

線形位相フィルタタイプ

フィルタ次数 n

係数の対称性

応答 H(f), f = 0

応答 H(f), f = 1 (Nyquist)

I型
偶数
偶数：

制約なし
制約なし

II型
奇数
制約なし
H(1) = 0

III型
偶数
奇数：

H(0) = 0
H(1) = 0

IV型
奇数
H(0) = 0
制約なし

線形位相フィルタタイプ	フィルタ次数 n	係数の対称性	応答 H(f), f `=` 0	応答 H(f), f `=` 1 (Nyquist)
I型	偶数	偶数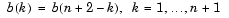：	制約なし	制約なし
II型	奇数	制約なし	H(1) `=` 0
III型	偶数	奇数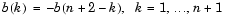：	H(0) `=` 0	H(1) `=` 0
IV型	奇数	H(0) `=` 0	制約なし

注意

つぎのワーニングメッセージを得た場合でも

-- Failure to Converge --
Probable cause is machine rounding error.

フィルタの設計は正しい場合があります。その周波数応答をチェックすることにより、設計を検証してください。

参考

butter
Butterworthアナログおよびディジタルフィルタの設計

cheby1
Chebyshev I型フィルタの設計(通過帯域リップル)

cheby2
Chebyshev II型フィルタの設計(遮断帯域リップル)

cremez
複素かつ非線形位相の等リップルFIRフィルタの設計

ellip
楕円フィルタの設計

fir1
ウィンドウベースの有限インパルス応答フィルタの設計－標準応答

fir2
ウィンドウベースの有限インパルス応答フィルタの設計－任意応答

fircls
複数帯域フィルタのための条件付き最小二乗FIRフィルタの設計

fircls1
ローパスおよびハイパス線形位相FIRフィルタのための条件付き最小2乗フィルタの設計

firls
最小2乗線形位相FIRフィルタの設計

firrcos
コサインロールオフFIRフィルタの設計

gremez
一般化remez最適FIRフィルタの設計

remezord
Parks-McClellan最適FIRフィルタの次数推定

yulewalk
巡回型ディジタルフィルタの設計

`butter`	Butterworthアナログおよびディジタルフィルタの設計
`cheby1`	Chebyshev I型フィルタの設計(通過帯域リップル)
`cheby2`	Chebyshev II型フィルタの設計(遮断帯域リップル)
`cremez`	複素かつ非線形位相の等リップルFIRフィルタの設計
`ellip`	楕円フィルタの設計
`fir1`	ウィンドウベースの有限インパルス応答フィルタの設計－標準応答
`fir2`	ウィンドウベースの有限インパルス応答フィルタの設計－任意応答
`fircls`	複数帯域フィルタのための条件付き最小二乗FIRフィルタの設計
`fircls1`	ローパスおよびハイパス線形位相FIRフィルタのための条件付き最小2乗フィルタの設計
`firls`	最小2乗線形位相FIRフィルタの設計
`firrcos`	コサインロールオフFIRフィルタの設計
`gremez`	一般化remez最適FIRフィルタの設計
`remezord`	Parks-McClellan最適FIRフィルタの次数推定
`yulewalk`	巡回型ディジタルフィルタの設計

参考文献

[1] Programs for Digital Signal Processing, IEEE Press, New York, 1979, Algorithm 5.1.

[2] Selected Papers in Digital Signal Processing, II, IEEE Press, New York, 1979.

[3] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, New York:, 1987, p. 83.

[4] Rabiner, L.R., J.H. McClellan, and T.W. Parks, "FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximations," Proc. IEEE 63 (1975).

[5] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1989, pp. 256-266.

rectpuls remezord