Signal Processing Toolbox

firls

条件付き最小2乗線形位相FIRフィルタの設計

表示

b = firls(n,f,a)
b = firls(n,f,a,w)
b = firls(n,f,a,'ftype')
b = firls(n,f,a,w,'ftype')

詳細

firlsは、希望する周波数帯域において、理想の区分的な線形関数とフィルタのゲイン応答との間の二乗和誤差の重み付き和を最小にする線形位相FIRフィルタを設計します。

b = firls(n,f,a) は、ベクトルfとaで表される周波数とゲインの関係を近似するn次のFIRフィルタの(n+1)個の係数を含んだ行ベクトルbを出力します。bに出力されるフィルタ係数、または、"タップ"は対称な関数をもちます。

これらは、I型(次数nが奇数)とII型(nが偶数)の線形位相フィルタになります。ベクトルfとaは、フィルタの周波数-ゲイン特性を設定します。

• fは、0〜1の範囲で設定される周波数点のベクトルで、1はサンプリング周波数の1/2(Nyquist周波数)です。周波数は、昇順でなければなりません。同一周波数点の設定は可能で、実際にこれを使って、関数fir1と関数fir2が箱形、すなわち、boxcarウィンドウを使って出力するフィルタと全く同じフィルタを設計することができます。
• aは、fに設定した点での希望する振幅を含んだベクトルです。

kが奇数の場合、点(f(k),f(k+1))の組の間の周波数で希望するゲイン関数は、点(f(k),a(k))と点(f(k+1),a(k+1))を結ぶ線分です。

kが偶数の場合、点(f(k),f(k+1))の組の間の周波数で希望するゲイン関数は設定されません。これらは、遷移領域、すなわち"配慮しない"領域です。

• f と aは、同じ長さです。この長さは、偶数でなければなりません。

firls は、常に、ナイキスト周波数で、通過帯域をもつ仕様に対して、偶数のフィルタ次数を使います。これは、奇数の次数の場合、ナイキスト周波数での周波数応答は、必ず0になるからです。n に偶数を設定すると、firls は、自動的に1を加えます。

希望のゲイン応答を定義する際のベクトルfとaの関係は、つぎのようになります。

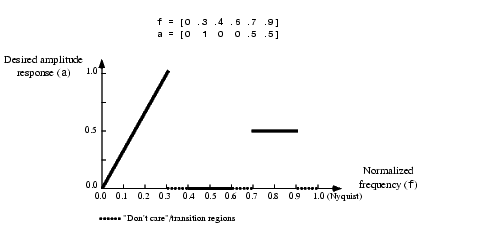
b = firls(n,f,a,w) は、ベクトルwの重みを使って、各周波数帯域の近似に重みを付けます。wの長さは、fとaの長さの半分になるため、帯域当たり厳密に1つの重みが存在します。

b = firls(n,f,a,'ftype') および

b = firls(n,f,a,w,'ftype') は、フィルタのタイプを設定します。ここで、ftypeは、つぎの文字列が設定できます。

• hilbert：奇数の対称な線形位相フィルタ(タイプIIIとタイプIV)

ベクトルbの中の出力係数は、b(k) = -b(n + 2 - k), k = 1, ... , n + 1の関係が成り立ちます。フィルタのこのクラスはHilbert変換子を含み、全帯域に渡り希望のゲイン1をもちます。

• differentiator：特別な重み付けの手法を使ったタイプIIIとタイプIVフィルタ

ゼロでない振幅帯域に対して、二乗和誤差は、低周波数での誤差が高周波数での誤差よりも小さくなるように(1/f)²の重みをもたせます。FIR微分器に対して、周波数に比例した振幅特性をもち、フィルタは相対的な二乗和誤差(誤差と希望する振幅の比の二乗和)を最小にしようとします。

例題

遷移帯域をもつ255次のローパスフィルタを設計します。

b = firls(255,[0 0.25 0.3 1],[1 1 0 0]);

つぎに、31個の係数微分器を設計します。

b = firls(30,[0 0.9],[0 0.9],'differentiator');

つぎに、区分的線形通過帯域をもつ24次の非対称フィルタを設計し、希望の周波数応答と実際の周波数応答をプロットします。

F = [0 0.3  0.4 0.6  0.7 0.9]; 
A = [0  1   0  0  0.5 0.5];
b = firls(24,F,A,'hilbert');
for i=1:2:6, 
   plot([F(i) F(i+1)],[A(i) A(i+1)],'- -'), hold on
end
[H,f] = freqz(b,1,512,2);
plot(f,abs(H)), grid on, hold off
legend('Ideal','firls Design')

アルゴリズム

参考文献[1]には、firlsが行う理論的手法が記述してあります。この関数は、MATLABの \演算子を使って、ほぼn/2 の大きさの内積行列を含んだ連立1次方程式を解きます。

この関数は、I型、II型、III型、およびIV型の線形位相フィルタを設計します。I型とII型は、それぞれnが偶数と奇数の場合のデフォルトですが、'hilbert'と'differentiator'フラグを付けると、III型(nが偶数の場合)とIV型(nが奇数の場合)フィルタを作成します。種々のフィルタタイプには、それぞれ異なる対称性と周波数応答に関する制約があります(詳細については、参考文献[2]を参照)。

線形位相フィルタタイプ	フィルタ次数 n	係数の対称性	応答 H(f), f = 0	応答 H(f), f = 1 (Nyquist)
タイプ I	偶数	even:	制約なし	制約なし
タイプ II	奇数		制約なし	H(1) = 0
タイプ III	偶数	奇数:	H(0) = 0	H(1) = 0
タイプ IV	奇数		H(0) = 0	制約なし

診断

誤った引数を使用した場合、つぎのようなワーニングメッセージが表示されます。

F must be even length.
F and A must be equal lengths.
Requires symmetry to be 'hilbert' or 'differentiator'.
Requires one weight per band.
Frequencies in F must be nondecreasing.
Frequencies in F must be in range [0,1].

より深刻なワーニングメッセージは、つぎのとおりです。

Warning: Matrix is close to singular or badly scaled.

これは、フィルタの長さと遷移幅の積が大きくなったときに生じる傾向があります。この場合、フィルタ係数bが希望のフィルタを表現していない可能性があります。その周波数応答を調べることにより、フィルタをチェックすることができます。

参考

fir1	ウィンドウベースの有限インパルス応答フィルタの設計 − 標準応答
fir2	ウィンドウベースの有限インパルス応答フィルタの設計 − 任意応答
firrcos	コサインロールオフParks-McClellan最適FIRフィルタの設計
remez	Parks-McClellan最適FIRフィルタの設計

参考文献

[1] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, 1987, pp. 54-83.

[2] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, pp. 256-266.

fircls1

firrcos