Signal Processing Toolbox

fir1

ウィンドウベースの有限インパルス応答フィルタの設計 − 標準応答

表示

b = fir1(n,Wn)
b = fir1(n,Wn,'ftype')
b = fir1(n,Wn,window)
b = fir1(n,Wn,'ftype',window)
b = fir1(...,'normalization')

詳細

fir1 は、ウィンドウを使った線形位相FIRディジタルフィルタの設計の古典的な方法を実現します(参考文献[1)。これは、標準的なローパス、バンドパス、ハイパス、およびバンドストップフィルタを設計します(任意周波数応答をもつウィンドウを使ったフィルタの場合、fir2を使用します)。

注意   任意の周波数応答をもつウィンドウをベースのフィルタを設計するfir2を使ってください。

b = fir1(n,Wn) は、n次のローパスFIRフィルタの(n+1)個の係数を含んだ行ベクトルbを出力します。これは、正規化したカットオフ周波数WnをもつHammingウィンドウをベースにした線形位相フィルタです。出力のフィルタ係数bは、zの次数の降順で出力されます。

カットオフ周波数Wnは、0と1の間の数値であり、1はサンプリング周波数の1/2(Nuyquist周波数)です。

Wnが2要素ベクトルWn = [w1 w2]の場合、fir1は通過帯域w1< < w2をもつバンドパスフィルタを出力します。

Wnが複数要素のベクトルWn = [w1 w2 w3 w4 w5 ... wn]の場合、fir1は帯域0<<w1,w1<< w2, ... , wn<< 1をもつn次の複数帯域フィルタを出力します。

デフォルトでは、フィルタはウィンドウ適用後に最初の通過帯域の中心部のゲインが1になるようにスケーリングされます。

b = fir1(n,Wn,'ftype') は、フィルタのタイプを設定します。ftypeは、つぎのように設定できます。

• 'high': カットオフ周波数Wnをもつハイパスフィルタ
• 'stop': Wnが2要素ベクトルWn = [w1 w2]の場合、バンドストップフィルタで、遮断帯域は、w1<< w2です。
• 'DC-1': 複数帯域フィルタの最初の帯域を通過帯域とします。
• 'DC-0': 複数帯域フィルタの最初の帯域を遮断帯域とします。

ハイパスおよびバンドストップ構成では、fir1は常に偶数のフィルタ次数を使用します。これは、次数が奇数の場合、Nyquist周波数での周波数応答が0になり、ハイパスフィルタやバンドストップフィルタには不適切になるためです。奇数値nを設定した場合、fir1は、その値を1だけ増分します。

b = fir1(n,Wn,window) は、列ベクトルwindowに設定されたウィンドウを設計に使用します。ベクトルwindowは、 n+1 の要素長でなければなりません。ウィンドウが設定されていなければ、fir1は、Hammingウィンドウ(hammingを参照)を使用します。

b = fir1(n,Wn,'ftype',window) は、ftypeとwindowの両パラメータを使います。

b = fir1(...,'normalization') は、フィルタの大きさを正規化するか否かを設定します。文字列'normalization'は、つぎのいずれかを設定することができます。

• 'scale' (デフォルト)：通過帯域の中心周波数で、フィルタの大きさの応答が0 dBになるように正規化します。
• 'noscale' : フィルタを正規化しません。

fir1で設計されたFIRフィルタの群遅延は、n/2となります。

アルゴリズム

fir1は、FIRフィルタ設計のウィンドウ法を使用します(参考文献[1])。 w(n)がウィンドウを示し(ここで、1 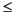n 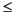N)、理想フィルタのインパルス応答がh(n)の場合(ここで、h(n)は、理想的な周波数応答の逆フーリエ変換)、ウィンドウを適用したディジタルフィルタ係数は、次式によって与えられます。

例題

通過帯域0.35 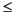w 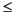0.65をもつ48次のFIRバンドパスフィルタを設計します。

b = fir1(48,[0.35 0.65]);
freqz(b,1,512)

chirp.matファイルは、大部分のパワーがfs/4より大きいか、または、Nyquist周波数の半分より大きい信号y を含んでいます。fs/4より低い信号成分を減衰させる34次のFIRハイパスフィルタを設計しましょう。このフィルタは、0.48のカットオフ周波数で、リップルが30 dBのChebyshevウインドウをもっているとします。

load chirp      % Load y and fs.
b = fir1(34,0.48,'high',chebwin(35,30));
freqz(b,1,512)

参考

filter	巡回型(IIR)または非巡回型(FIR)フィルタによるデータのフィルタリング
fir2	ウィンドウベースの有限インパルス応答フィルタの設計 − 任意応答
fircls	複数帯域フィルタのための条件付き最小2乗FIRフィルタの設計
fircls1	ローパスおよびハイパス線形位相FIRフィルタのための条件付き最小2乗フィルタの設計
firls	条件付き最小2乗線形位相FIRフィルタの設計
freqz	ディジタルフィルタの周波数応答
kaiserord	Kaiserウィンドウを使ったfir1のパラメータ推定
remez	Parks-McClellan最適FIRフィルタの設計

参考文献

[1] Programs for Digital Signal Processing, IEEE Press, New York, 1979. Algorithm 5.2.

filtic

fir2