Signal Processing Toolbox

pmusic

MUSIC アルゴリズムを使った擬似スペクトルの推定

表示

[S,w] = pmusic(x,p)
[S,w] = pmusic(...,nfft)
[S,f] = pmusic(x,p,nfft,fs))
[S,f] = pmusic(...,'corr')
[S,f] = pmusic(x,p,nfft,fs,nwin,noverlap)
[...] = pmusic(...,'range')
[...,v,e] = pmusic(...)
pmusic(...)

詳細

[S,w] = pmusic(x,p) は、MUSIC(Multiple Signal Classification)アルゴリズムを実現し、入力信号xの擬似スペクトルSと擬似スペクトルが計算された点を正規化した周波数(ラジアン/サンプル)で表したベクトルwを出力します。擬似スペクトルは、入力データxに関連した相関行列の固有ベクトルを使って計算されます。xは、つぎのいずれかに対応する入力信号です。

• 行または列ベクトルを使って、信号の一つの観測を表す
• xの各行が信号(たとえば、アレープロセッシングで使われるように、各行がセンサの配列の一出力)を表す長方形の配列、たとえば、x'*xは、相関行列です。

注意    関数corrmtxを使って、配列xを作成します。

つぎのいずれかとして、2番目の入力引数pを設定できます。

• スカラ整数：この場合、信号サブ空間の次元はpです。
• 2要素ベクトル：この場合、pの2番目の要素 p(2)は、信号の相関行列の固有値の中の最小な値、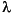_minを乗算するスレッシュホールドを表しています。スレッシュホールド 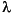_min*p(2)より小さい固有値は、ノイズのサブ空間に割り当てます。この場合、p(1)は、信号サブ空間の最大次元を設定します。

pの中の2番目の要素のスレッシュホールドパラメータは、非常に柔軟性をもち、ノイズサブ空間と信号サブ空間の割り当てをコントロールします。

S と wは、 同じ長さです。一般に、FFTの長さと入力xの値(実数/複素数)により、計算されるSの長さと対応する正規化された周波数の範囲を決めることができます。つぎの表は、この書式で、S(とw)の長さと対応する正規化された周波数の範囲を示しています。

表 7-29:   長さ256(デフォルト)のFFTに対する S 特性

実数/複素数入力データ	Sとwの長さ	対応している正規化された周波数の範囲
実数値	129	[0, ]
複素数値	256	[0, 2)

[S,w] = pmusic(...,nfft) は、整数nfftを使って、擬似スペクトルの推定に使用するFFTの長さを設定します。nfftに対するデフォルト値は、256です。

つぎの表は、この書式に対するSとwの長さとwに対する周波数の範囲を示しています。

表 7-30:  S と周波数ベクトルの特性

実数/複素数入力データ	nfft 偶数/奇数	S と wの長さ	w の範囲
実数値	偶数	(nfft/2 + 1)	[0, ]
実数値	奇数	(nfft + 1)/2	[0, )
複素数値	偶数または奇数	nfft	[0, 2)

[S,f] = pmusic(x,p,nfft,fs)) は、ベクトルSに推定した擬似スペクトルを出力し、それに対応する周波数(Hz単位)ベクトルをfに出力します。空ベクトル[]を設定すると、サンプリング周波数はデフォルトの1Hzになります。

fに対する周波数範囲は、nfftとfsと入力xの値(実数/複素数/個数)に依存します。S(とf)の長さは、表 7-30 Sと周波数ベクトルの特性 と同じです。つぎの表は、この書式用の f に対する周波数の範囲を示しています。

表 7-31:  fsを設定した S と周波数ベクトルの特性

実数/複素数入力データ	nfft 偶数/奇数	fの範囲
実数値	偶数	[0, fs/2]
実数値	奇数	[0, fs/2)
複素数値	偶数または奇数	[0, fs)

[S,f] = pmusic(...,'corr') は、信号データの行列ではなく、相関行列として入力引数xを解釈します。この書式では、xは正方行列で、その固有値はすべて非負です。

[S,f] = pmusic(x,p,nfft,fs,nwin,noverlap) は、引数nwinを使って、長方形ウインドウの長さを設定するスカラ整数、または、ウインドウ係数を設定する実数値ベクトルのいずれかを設定します。nwinと組み合わせてスカラ整数noverlapを使用することで、入力サンプルに連続的にある重なりを保ってウインドゥを適用することができます。noverlapは、xが行列の場合、使用できません。デフォルト値は、nwinが2*p(1)、noverlapはnwin-1です。

この書式で、入力データxは、相関行列固有値を推定するために使用する行列が型作られる前に、分割され、ウインドウが適用されます。データの分割は、nwinとnoverlapとxの型に依存します。結果ウインドウを適用された各部分に関するコメントをつぎの表に記述されます。

表 7-32:  xとnwinに依存したウインドウを適用されたデータ

入力データ x	nwin の型	ウインドウを適用されたデータ
データベクトル	スカラ	長さは、nwinです。
データベクトル	係数ベクトル	長さは、nwinです。
データ行列	スカラ	データには、ウインドウが適用されていません。
データ行列	係数ベクトル	length(nwin) は、xの列の長さと同じで、noverlapは使われません。

この書式に関する関連した情報に対しては、表 7-33の入力データと書式に依存した固有ベクトルの長さを参照してください。

注意    引数 nwin と noverlapは、文字列'corr'を書式内に含ませると無視されます。

[...] = pmusic(...,'range') は、fまたは wの中に、周波数値の範囲を設定できます。この書式は、xが実数の場合に有効です。'range' には、つぎのいずれかを設定することができます。

• 'whole': 周波数範囲[0,fs)上で擬似スペクトルを計算します。これは、xが複素数値の場合の周波数範囲のデフォルトです。
• fsに空行列を設定する場合、周波数範囲は、[0,1)になります。
• fsを設定しない場合、周波数範囲は、[0, 2)になります。
• 'half':xが実数の場合、設定した周波数範囲上で擬似スペクトルを計算します。これは、xが実数の場合の周波数範囲のデフォルトです。

注意    引数'range'または'corr'は、引数pの後の場合、任意の位置に設定することができます。

[...,v,e] = pmusic(...) は、ノイズ固有ベクトルの行列vを出力し、ベクトルeに関連した固有値を出力します。vの列は、(大きさ size(v,2)の)ノイズサブ空間を構成します。信号サブ空間の次元は、size(v,1)-size(v,2)です。この書式で、eは相関行列の推定された固有値ベクトルです。

pmusic(...) は、出力引数を設定しない場合、カレントフィギュアウインドウ内に擬似スペクトルをプロットします。

注意

擬似スペクトルの推定の過程で、関数pmusicは、信号の相関行列の固有ベクトル v_j と固有値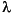_j からノイズと信号のサブ空間を計算します。これらの固有値の中の最小のものが、スレッシュホールドパラメータp(2)と共に使われ、ノイズのサブ空間の大きさに影響を同じように与えます。

関数pmusicで計算される固有ベクトルの長さnは、信号のサブ空間の次元とノイズのサブ空間の次元との和です。この固有ベクトルの長さは、入力(信号データまたは相関行列)とユーザが使用する書式に依存します。

つぎの表は、入力引数への固有ベクトル長の依存度をまとめたものです。

表  7-33:  入力データと書式に依存した固有ベクトルの長さ 

入力データ x の形成	書式に関するコメント	固有ベクトルの長さ n
行または列ベクトル	nwinは、スカラ整数として設定	nwin
行ベクトルまたは列ベクトル	nwinは、ベクトルとして設定されています。	length(nwin)
行ベクトルまたは列ベクトル	nwin は、設定されていません。	2*p(1)
l行m列の行列	nwinがスカラの場合、使われません。また、ベクトルの場合、length(nwin)はmと等しくなります。	m
m行m列のの非負の正定行列	文字列'corr'が設定され、nwinは使われません。	m

ある影響を加えるために、p(2)>1としたい場合、nwin > p(1)または(length(nwin) > p(1))のいずれかを設定しなければなりません。

例題

例題 1: サンプリングを設定していない関数 pmusic

この例題は、信号サブ空間に存在する2つの実数正弦波を仮定して、ある信号ベクトルxを解析します。この場合、各実数正弦波は、2つの複素指数の和で表されるので、信号のサブ空間の次元は4です。

randn('state',0);
n = 0:199;
x = cos(0.257*pi*n) + sin(0.2*pi*n) + 0.01*randn(size(n));
pmusic(x,4)

例題 2: サンプリング周波数とサブ空間次元を指定

この例題は、同じ信号ベクトルに最小値より10%の固有値をカットしたベクトルx を解析します。p(1) = Infは、信号/ノイズのサブ空間の決定に、スレッシュホールドp(2)をベースにしたものを使います。引数nwinを使って、長さ7の固有ベクトルを設定し、サンプリング周波数fsを 8 kHzに設定します。

randn('state',0);
n = 0:199;
x = cos(0.257*pi*n) + sin(0.2*pi*n) + 0.01*randn(size(n));
[P,f] = pmusic(x,[Inf,1.1],[],8000,7); % ウインドウの長さ = 7

例題 3: 相関行列を入力

スペクトル密度を計算するために、正定相関行列Rを入力します。デフォルトの長さ256サンプルを使います。

R = toeplitz(cos(0.1*pi*[0:6])) + 0.1*eye(7);
[P,f] = pmusic(R,4,'corr');

例題 4: 関数 corrmtx を使って、データから作成した信号データ行列を入力します。

関数corrmtxを使って、データから作成した信号データ行列 Xmを入力します。

randn('state',0);
n = 0:699;
x = cos(0.257*pi*(n)) + 0.1*randn(size(n));
Xm = corrmtx(x,7,'mod');
[P,w] = pmusic(Xm,2);

例題 5: ウインドウを使用して、信号データ行列の影響を作成

同じ信号を使いますが、ウインドウを適用する入力引数を使って、100行7列のデータ行列を作成します。そして、FFTの長さを512とします。

randn('state',0);
n = 0:699;
x = cos(0.257*pi*(n)) + 0.1*randn(size(n));
[PP,ff] = pmusic(x,2,512,[],7,0);

アルゴリズム

MUSICと言う名前は、MUltiple SIgnal Classification に由来します。MUSICアルゴリズムは、信号または信号の相関行列から Schmidtの固有空間解析法(参考文献[1])を使って、擬似スペクトルを計算します。アルゴリズムは、信号の周波数成分を計算するため、信号の相関行列の固有空間解析を行います。このアルゴリズムは、正弦波に加算的な白色ガウスノイズが加わったような信号に特に効果的に働きます。相関行列を設定していない場合は、信号の相関行列の固有値や固有ベクトルが計算されます。

MUSIC擬似スペクトルは、次式で与えられます。

ここで、Nは、固有ベクトルの次元で、v_k は相関行列のk番目の固有ベクトルです。整数pは、信号のサブ空間の次元です。そのため、和の中で使われる固有ベクトルv_kは、相関行列の最小の固有値に対応します。PSD推定の中で使われる固有ベクトルは、ノイズ空間を構成します。ベクトルe(f)は、複素指数の型をし、そのため、内積

は、フーリエ変換になります。これは、PSD推定の計算で使われるものです。FFTは、各v_kに対して計算され、大きさの二乗の和が計算され、スケーリングします。

参考

corrmtx	相関行列の計算用に入力データを整形
pburg	Burg法を使ったパワースペクトル密度の計算
peig	固有ベクトル法を使った擬似スペクトルの推定
periodogram	ピリオドグラムを使ったパワースペクトル密度の計算
pmtm	マルチテーパ法を使ったパワースペクトル密度の計算
prony	時間領域IIRフィルタ設計に対するProny法
psdplot	パワースペクトル密度データのプロット
pwelch	Welch法を使ったパワースペクトル密度の計算
rooteig	ルート固有ベクトル法を使った周波数とパワーの計算
rootmusic	ルートMUSICアルゴリズムを使った周波数とパワーの計算

参考文献

[1] Marple, S.L. Digital Spectral Analysis, Englewood Cliffs, NJ, Prentice-Hall, 1987, pp. 373-378.

[2] Schmidt, R.O, "Multiple Emitter Location and Signal Parameter Estimation," IEEE Trans. Antennas Propagation, Vol. AP-34 (March 1986), pp. 276-280.

[3] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, Englewood Cliffs, NJ, 1997.

pmtm

poly2ac