| Signal Processing Toolbox | |
ピリオドグラムを使って、信号のパワースペクトル密度(PSD)を計算
表示
[Pxx,w]=periodogram(x) [Pxx,w]=periodogram(x,window) [Pxx,w]=periodogram(x,window,nfft) [Pxx,f]=periodogram(x,window,nfft,fs) [Pxx,...]=periodogram(x,...,'range') periodogram(...)
詳細
[Pxx,w は、ピリオドグラムを使って、数列] = periodogram(x)
xのパワースペクトル密度(PSD)を計算し、出力します。パワースペクトル密度は、パワー/ラジアン/サンプルの単位で計算されます。対応する周波数ベクトルwは、ラジアン/サンプルで計算され、Pxxと同じ長さになります。
入力ベクトル x が実数値の場合、片側PSDをデフォルトで計算し、複素数値の場合、両側PSDを計算します。
一般的に、FFTの長さNと入力xの値(実数/複素数)により、Pxxの長さと対応する正規化された周波数の範囲が決まります。この書式で、FFT(デフォルト)の長さNは、256より長くなり、xの長さを超える2のベキ乗数の内一番小さいものになります。つぎの表は、この書式用のPxxの長さと対応する正規化された周波数の範囲を示しています。
| 実数/複素数入力データ |
Pxxの長さ |
対応する正規化した周波数の範囲 |
| 実数値 |
(N/2) +1 |
[0,  ] |
| 複素数値 |
N |
[0, 2) |
[Pxx,w] は、修正ピリオドグラム法を使って計算したPSDを = periodogram(x,window)
Pxxに出力します。ベクトルwindowは、入力信号の修正ピリオドグラムを計算するのに使用するウインドウの係数を設定するものです。2つの入力引数は共に、同じ長さのベクトルである必要があります。2番目の引数windowを設定しない場合、または、空ベクトル[]で設定する場合、長方形のウインドウ(boxcarを参照)がデフォルトで使われます。この状態で、ピリオドグラムが計算されます。
[Pxx,w] は、FFTの長さを整数 = periodogram(x,window,nfft)
nfftで設定して、修正ピリオドグラムを使って、PSDを計算します。nfftに[]ベクトルを設定すると、上記の書式に関する表の一覧でのNに関するデフォルト値を使います。
Pxxの長さとwに対する周波数の範囲は、nfftと入力xの値(実数/複素数/個数)に依存します。つぎの表は、この書式用のPxxの長さとwの周波数の範囲です。
| 実数/複素数入力データ |
nfft 偶数/奇数 |
Pxxの長さ |
wの範囲 |
| 実数値 |
偶数 |
(nfft/2 + 1) |
[0, ] |
| 実数値 |
奇数 |
(nfft + 1)/2 |
[0, ) |
| 複素数値 |
偶数または奇数 |
nfft |
[0, 2) |
注意
関数periodogramは、ピリオドグラムを計算するために、ウインドウを適用したデータ(x.*window)のnfft点のFFTを使います。設定したデータが、nfftより短い場合、x.*windowはFFTを計算するためにゼロを加え、長い場合は打ち切ります。 |
[Pxx,f] は、PSDベクトル( = periodogram(x,window,nfft,fs)
Pxx)と対応する周波数ベクトル(f)を計算するために、ヘルツ単位の整数で設定したサンプリング周波数を使います。この場合、周波数ベクトルに対する単位は、Hzです。作成したスペクトル密度は、パワー/ヘルツで計算されます。fsを空ベクトル[]で設定すると、サンプリング周波数は、デフォルトの1 Hzになります。
fに対する周波数範囲は、nfftとfs、入力値x(実数/複素数/個数)に依存します。Pxxの長さは、上の表と同じです。この書式用に、つぎの表にfに対する周波数範囲を示します。
| 実数/複素数入力データ |
nfft 偶数/奇数 |
fの範囲 |
| 実数値 |
偶数 |
[0, fs/2] |
| 実数値 |
奇数 |
[0, fs/2) |
| 複素数値 |
偶数または奇数 |
[0, fs) |
[Pxx,f] または、[Pxx,w] = periodogram(x,window,nfft,fs,'range')
= periodogram(x,window,nfft,'range') は、周波数値の範囲を f と w に出力します。 x が実数の場合、この書式は有効です。'range'には、つぎのいずれかを使用することができます。
'twosided': 周波数範囲[0,fs)で両側PSDを計算します。これは、xが複素数の場合の周波数範囲のデフォルトの設定です。fsを空ベクトル[]とする場合、周波数範囲は[0,1)です。
fsを設定していない場合、周波数範囲は[0, 2)です。'onesided': 実数xに対して設定した周波数範囲上での片側PSDを計算します。これは、xが実数の場合の周波数範囲のデフォルトの設定です。periodogram(...)
は、カレントフィギュアウインドウに、単位周波数に対して dB表示でパワースペクトル密度をプロットします。プロット上の周波数範囲は、ユーザが使用する書式に適した出力w(または f)の範囲と同じものになります。
例題
加算的なノイズを含んだ200 Hz の信号のピリオドグラムを、デフォルトのウインドウを使って、計算します。
randn('state',0);
Fs = 1000;
t = 0:1/Fs:.3;
x = cos(2*pi*t*200)+0.1*randn(size(t));
periodogram(x,[],'twosided',512,Fs)
アルゴリズム
数列[x1, ... , xn] に対するピリオドグラムは、つぎの式で与えられます。
|
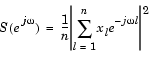
(7-1) |
この式は、数列[x1, ... , xn] で定義した信号のパワースペクトルを行います。
ユーザの信号列に、ウインドウ [w1, ... , wn]で重み付けを行う場合、重み付けピリオドグラムまたは修正ピリオドグラムは、つぎのように定義されます。
|
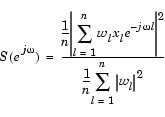
(7-2) |
また、関数periodogramは、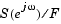
のようにパワースペクトル密度を計算するため 、nfft点のFFTを使います。ここで、Fは、
です。 
fsです。 参考
|
Burg法を使ったパワースペクトル密度を計算 |
|
共分散法を使ったパワースペクトル密度の計算 |
|
固有ベクトル法を使った擬似スペクトルの推定 |
|
修正共分散法を使ったパワースペクトル密度の計算 |
|
マルチテーパ法を使ったパワースペクトル密度の計算 |
|
MUSIC アルゴリズムを使った擬似スペクトルの推定 |
|
パワースペクトル密度データのプロット |
|
Welch法を使ったパワースペクトル密度の計算 |
|
Yule-Walker AR法を使ったパワースペクトル密度の計算 |
参考文献
[1] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, 1997, pp. 24-26.
[2] Welch, P.D, "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms," IEEE Trans. Audio Electroacoustics, Vol. AU-15 (June 1967), pp. 70-73.
[3] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, pp. 730-742.
| | peig | pmcov | |