

| Signal Processing Toolbox |   |
Welch法を使った信号のパワースペクトル密度(PSD)の推定
表示
[Pxx,w]=pwelch(x) [Pxx,w]=pwelch(x,nwin) [Pxx,w]=pwelch(x,nwin,noverlap) [Pxx,w]=pwelch(x,nwin,noverlap,nfft) [Pxx,f]=pwelch(x,nwin,noverlap,nfft,fs) [...]=pwelch(x,nwin,noverlap,...,'range') pwelch(...)
詳細
[Pxx,w] は、スペクトル推定のWelchの平均化修正ピロオドグラム法を使って、入力信号ベクトル = pwelch(x)
xのパワースペクトル密度Pxxを計算します。つぎの書式を使います。
xは、同じ長さの8つの部分(お互い50%の重なりをもつ)に分割します。hammingを参照)を適用します。パワースペクトル密度は、パワー/ラジアン/サンプル単位で計算されます。対応する周波数ベクトルwは、ラジアン/サンプルで計算され、Pxxと同じ長さをもっています。
xが実数値入力ベクトルの場合、片側PSDが計算され、複素数の場合、両側PSDが計算されます。
一般的に、FFTの長さNと入力xの値(実数/複素数)により、Pxxの長さと対応する正規化された周波数の範囲を決めます。この書式で、FFTの(デフォルト)の長さNは、256より長くなり、xの長さを超える2のベキ乗数の内一番小さいものになります。つぎの表は、この書式用のPxxの長さと対応する正規化された周波数の範囲を示しています。
| 実数/複素数入力データ |
Pxxの長さ |
対応する正規化された周波数の範囲 |
| 実数値 |
(N/2) +1 |
[0,  ] ] |
| 複素数値 |
N |
[0, 2 ) ) |
[Pxx,w] は、つぎのいずれかを使って、修正ピリオドグラムを計算します。 = pwelch(x,nwin)
nwinが正の整数の場合、nwinはHammingウインドウの長さnwinがベクトルの場合、ウインドウに重みも設定できます。
この書式では、入力ベクトルxは、お互い50%の重なりをもちながら、ある整数倍で、同じ長さをもつように分割し、残りの部分は、削除します。nwinに空ベクトル[]を設定すると、信号データは、8つに分割され、その各々にHammingウインドウが適用されます。
[Pxx,w] は、 = pwelch(x,nwin,noverlap)
nwinに従ってxを分割し、整数noverlapを使って、隣同士の分割で共有する部分の信号のサンプル数を設定します。引数noverlapは、ユーザが設定するウインドウの長さよりも短い必要があります。noverlapを空ベクトル[]に設定すると、pwelchは、デフォルトの重ね合わせが50%になるように、xの分割を行います。
[Pxx,w] は、Welch法を使って、PSDを計算しますが、FFTの長さを整数 = pwelch(x,nwin,noverlap,nfft)
nfftで設定することができます。nfftを空ベクトル[]で設定すると、上記の書式でリストされているNに対するデフォルト値を使います。
Pxxの長さとwの周波数範囲は、nfftと入力xの値(実数/複素数/個数)に依存します。つぎの表は、この書式でのPxxの長さとwの周波数範囲を示しています。
| 実数/複素数入力データ |
nfft 偶数/奇数 |
Pxxの長さ |
w の範囲 |
| 実数値 |
偶数 |
(nfft/2 + 1) |
[0,  ] ] |
| 実数値 |
奇数 |
(nfft + 1)/2 |
[0,  ) ) |
| 複素数値 |
偶数または奇数 |
nfft |
[0, 2 ) ) |
[Pxx,f] は、PSDベクトル( = pwelch(x,nwin,noverlap,nfft,fs)
Pxx)と対応する周波数ベクトル(f)を計算するためにヘルツ単位で設定したサンプリング周波数fsを使います。計算されるスペクトル密度は、パワー/Hzの単位です。fsを空ベクトル[]とすると、サンプリング周波数は、デフォルトの1 Hzです。
fに関する周波数範囲は、nfftとfsと入力xの値(実数/複素数/個数)に依存します。Pxxの長さは、上記の表の中のものと同じです。つぎの表は、この書式を使ったfに対する周波数範囲を示しています。
| 実数/複素数入力データ |
nfft 偶数/奇数 |
fの範囲 |
| 実数値 |
偶数 |
[0, fs/2] |
| 実数値 |
奇数 |
[0, fs/2) |
| 複素数値 |
偶数または奇数 |
[0, fs) |
[...] は、周波数の範囲を設定することができます。この書式は、 = pwelch(x,nwin,noverlap,...,'range')
xが実数の場合に有効です。'range'には、つぎのいずれかを設定することができます。
'twosided': 周波数範囲[0,fs)で両側PSDを計算します。これは、xが複素数の場合の周波数範囲のデフォルトの設定です。fsを空ベクトル[]とする場合、周波数範囲は[0,1)です。 fsを設定していない場合、周波数範囲は[0, 2 )です。
)です。 'onesided': 実数xに対して設定した周波数範囲上での片側PSDを計算します。これは、xが実数の場合の周波数範囲のデフォルトの設定です。文字引数'range' は、引数noverlapの後の場合、任意の位置に設定することができます。
pwelch(x,...) は、カレントフィギュアウインドウに周波数に対してdB表示のPSDをプロット表示します。
例題
正弦波とノイズから構成される信号のPSDを計算しましょう。サンプリング周波数は、1000 Hzです。32のサンプルのオーバラップをもった長さ33サンプルのウインドウとデフォルトのFFTの長さを使って、両側PSD計算結果を表示します。
randn('state',0);
Fs = 1000; t = 0:1/Fs:.3;
x = cos(2*pi*t*200)+randn(size(t)); % 200Hzの正弦波とノイズから構成
pwelch(x,33,32,[],Fs,'twosided')
アルゴリズム
pwelchは、Welch法を使って、パワースペクトル密度を計算します。
x は、nwinとnoverlap(またはデフォルト値)に従って、k個のオーバラップした部分に分割します。
xを分割したものの各々に適用されます。
nfft点のFFTの計算は、ウインドウを適用したデータに対して実行されます。
periodogramのリファレンスの式 7-22を参照してください)。
 )を作ります。
)を作ります。
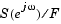 、ここで、Fは、
、ここで、Fは、
nwinを設定していないか、または、nwinを空ベクトル[]とすると、8です。 nwinを空でないベクトルまたはスカラで設定すると、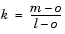 です。
です。この方程式の中で、mは信号ベクトルxの長さで、oはオーバラップのサンプル数(noverlap)で、lは各部分の長さ(ウインドウの長さ)です。
参考
|
Burg法を使って、パワースペクトル密度を計算 |
|
共分散法を使ったパワースペクトル密度の計算 |
|
固有ベクトル法を使った擬似スペクトルの推定 |
|
ピリオドグラムを使ったパワースペクトル密度の計算 |
|
修正共分散法を使ったパワースペクトル密度の計算 |
|
マルチテーパ法を使ったパワースペクトル密度の計算 |
|
MUSIC アルゴリズムを使った擬似スペクトルの推定 |
|
パワースペクトル密度データのプロット |
|
Yule-Walker AR法を使ったパワースペクトル密度の計算 |
参考文献
[1] Hayes, M., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, 1996.
[2] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, Englewood Cliffs, NJ, 1997, pp. 52-54.
[3] Welch, P.D, "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms," IEEE Trans. Audio Electroacoustics, Vol. AU-15 (June 1967), pp. 70-73.
 | pulstran | pyulear |  |