Signal Processing Toolbox

lp2bp

ローパスアナログフィルタからバンドパスアナログフィルタへの変換

表示

[bt,at] = lp2bp(b,a,Wo,Bw)
[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw)

詳細

lp2bpは、1ラジアン/秒のカットオフ周波数をもつアナログローパスフィルタのプロトタイプを、希望の帯域幅と中心周波数をもつバンドパスフィルタに変換します。変換は、関数butter、 cheby1、 cheby2およびellipに対するディジタルフィルタの設計過程の1ステップです。

lp2bpは、2つの異なる線形システム表現(伝達関数型および状態空間(State space)型)で変換を行うことができます。いずれの場合も、入力システムは、アナログフィルタのプロトタイプでなければなりません。

伝達関数型(多項式)

[bt,at] = lp2bp(b,a,Wo,Bw) は、多項式係数によって与えられるアナログローパスフィルタのプロトタイプを、中心周波数Woと帯域幅Bwをもつバンドパスフィルタに変換します。行ベクトルbおよびaは、プロトタイプの分子および分母の係数をsの次数の降順で設定します。

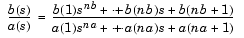
スカラWoおよびBwは、中心周波数と帯域幅をラジアン/秒単位で設定します。低い方の帯域エッジw1と高い方の帯域エッジw2をもつフィルタに対して、Wo = sqrt(w1*w2)とBw = w2-w1を使用してください。

lp2bpは、周波数変換されたフィルタを行ベクトルbtおよびatに出力します。

状態空間(State space)型

[At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw) は、行列A, B, C, Dの連続系状態空間(State space)ローパスフィルタのプロトタイプ

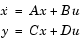
を、中心周波数 Wo と帯域幅 Bw をもつバンドパスフィルタに変換します。低い方の帯域エッジ w1 と高い方の帯域エッジ w2 をもつフィルタに対しては、Wo = sqrt(w1*w2)とBw = w2-w1を使用してください。

このバンドパスフィルタは、行列At, Bt, Ct, Dtに出力されます。

アルゴリズム

lp2bpは、古典的なアナログフィルタ周波数変換を高精度で処理を行う状態空間(State space)型公式を使っています。つぎの状態空間システムを考えます。

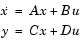
ここで、uは入力、xは状態ベクトル、yは出力です。最初の方程式のLaplace変換は、つぎのようになります。

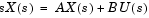
このとき、バンドパスフィルタが中心周波数₀と帯域幅B_wをもつ場合、標準のs領域の変換は、つぎのようになります。

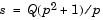
ここで、Q = ₀/B_wおよびp = s/₀です。これをLaplace変換した状態空間(State space)方程式のs に代入し、演算子p を d/dtと考えます。

または、

このとき、つぎのように定義します。

これを代入すると次式が導かれます。

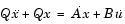
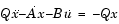
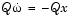
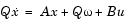
最後の2つの方程式により、状態方程式が得られます。これらを標準型で記述し、pで表される時間/周波数スケーリングを回復させるために₀を微分方程式に乗算し、バンドパスフィルタの状態行列を求めます。

Q = Wo/Bw; [ma,na] = size(A);
At = Wo*[A/Q eye(ma,na);-eye(ma,na) zeros(ma,na)];
Bt = Wo*[B/Q; zeros(ma,nb)];
Ct = [C zeros(mc,ma)];
Dt = d;

lp2bpへの入力が伝達関数型の場合、関数はそれを状態空間(State space)型に変換してから、このアルゴリズムを適用します。

参考

bilinear	双1次変換を使った変数のマッピング
impinvar	アナログ/ディジタルフィルタ変換のインパルス不変応答変換法
lp2bs	ローパスフィルタからバンドストップアナログフィルタへの変換
lp2hp	ローパスフィルタからハイパスアナログフィルタへの変換
lp2lp	ローパスアナログフィルタのカットオフ周波数の変更

levinson

lp2bs