

| Signal Processing Toolbox |   |
表示
[zd,pd,kd]=bilinear(z,p,k,fs) [zd,pd,kd]=bilinear(z,p,k,fs,Fp) [numd,dend]=bilinear(num,den,fs) [numd,dend]=bilinear(num,den,fs,Fp) [Ad,Bd,Cd,Dd]=bilinear(A,B,C,D,fs) [Ad,Bd,Cd,Dd]=bilinear(A,B,C,D,fs,Fp)
詳細
双1次変換とは、変数の数学的なマッピングです。ディジタルフィルタ処理では、これは、s(アナログ)平面をz(ディジタル)平面にマッピングする標準的な方法です。双1次変換は、古典的なフィルタ設計手法を使って設計されたアナログフィルタを離散の等価なフィルタに変換します。
双1次変換では、次式によりs平面をz平面にマッピングします。
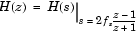
この変換では、次式を使って、j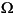 軸を単位円周上(exp(j
軸を単位円周上(exp(j )に繰り返しマッピングします。ここで、
)に繰り返しマッピングします。ここで、 は、-
は、- から
から で、
で、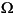 は-
は-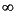 から
から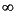 の範囲です。
の範囲です。
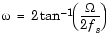
bilinearには、プリワーピングを設定するオプションパラメータFpを付加することができます。Fpは、"基準"周波数、すなわちマッピング処理の前後で周波数応答が正確に一致する周波数をヘルツ単位で示します。プリワーピングモードでは、双1次変換は、次式によりs平面をz平面にマッピングします。
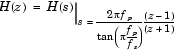
プリワーピングオプションを付加すると、bilinearは次式を使って、j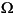 軸を単位円周上(exp(j
軸を単位円周上(exp(j )に繰り返しマッピングします。ここで、
)に繰り返しマッピングします。ここで、 は、-
は、- から
から で、
で、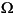 は-
は-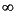 から+
から+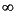 の範囲です。
の範囲です。
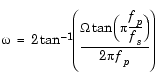
プリワーピングモードでは、bilinearはs平面の周波数2 fs(ラジアン/秒)を、z平面の2
fs(ラジアン/秒)を、z平面の2 fp(ラジアン/秒)に一致させます。
fp(ラジアン/秒)に一致させます。
関数bilinearは、3つの異なる線形システム表現(零点-極-ゲイン、伝達関数、および状態空間型)で機能します。
零点-極-ゲイン
[zd,pd,kd] = bilinear(z,p,k,fs)
および
[zd,pd,kd] = bilinear(z,p,k,fs,Fp)
は、z、p、およびkで設定されるs領域の伝達関数を離散の等価な関数に変換します。入力zおよびpは零点と極を含む列ベクトルで、kはスカラゲインです。fsは、ヘルツ単位のサンプリング周波数です。bilinearは、列ベクトルzdとpdとスカラkdに、離散の等価な関数を出力します。Fpは、プリワーピングに関するオプションの基準周波数をヘルツ単位で表したものです。
伝達関数
[numd,dend] = bilinear(num,den,fs)
および
[numd,dend] = bilinear(num,den,fs,Fp)
は、numおよびdenによって与えられるs領域伝達関数を離散の等価な関数に変換します。行ベクトルnumおよびdenは、つぎのように分子および分母の係数をsの次数の降順にそれぞれ設定します。
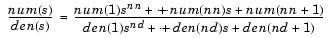
fsは、ヘルツ単位のサンプリング周波数です。bilinearは、離散の等価な関数を行ベクトルnumdおよびdendにz の次数の降順(z-1の昇順)に出力します。Fpは、プリワーピングに関するオプションの基準周波数をヘルツ単位で表したものです。
状態空間
[Ad,Bd,Cd,Dd] = bilinear(A,B,C,D,fs)
および
[Ad,Bd,Cd,Dd] = bilinear(A,B,C,D,fs,Fp)
は、行列A、B、C、Dの連続系状態空間システム
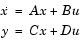
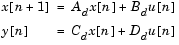
fsは、ヘルツ単位のサンプリング周波数です。bilinearは、離散の等価なシステムを行列Ad、Bd、Cd、Ddに出力します。Fpは、プリワーピングに関するオプションの基準周波数をヘルツ単位で表したものです。
アルゴリズム
bilinearは、与えられた入力線形システムの形式に応じて、2つのアルゴリズムのどちらかを使用します。一つのアルゴリズムは、零点-極-ゲイン型を処理し、もう一つのアルゴリズムは、状態空間型を処理します。伝達関数表現の場合には、bilinearは、まず状態空間型に変換してから、この変換を実行し、得られた状態空間システムを伝達関数型に逆変換します。
零点-極-ゲインアルゴリズム
零点-極-ゲイン型のシステムの場合、bilinearは、つぎの4つのステップを実行します。
Fpが存在する場合、k = 2*pi*Fp/tan(pi*Fp/fs)とし、存在しない場合、k = 2*fsとします。
z = z(find(finite(z)));
pd=(1+p/k)./(1-p/k); zd=(1+z/k)./(1-z/k); kd=real(k*prod(fs-z)./prod(fs-p));
状態空間アルゴリズム
状態空間型のシステムの場合、bilinearは、つぎの2つのステップを実行します。
Fpが存在する場合、k = 2*pi*Fp/tan(pi*Fp/fs)とし、存在しない場合、k = 2*fsとします。
A、B、C、およびDを使って、Ad、Bd、Cd、およびDdを計算します。
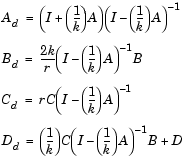
bilinearは、通常のMATLABステートメントを使って、これらの関係を実現します。スカラrは任意です。bilinearは、結果求まるシステム中で、良好な量子化ノイズを保証するため、sqrt(2/k)を使います。
診断
bilinearは、分子の次数が分母の次数以下であることを必要とします。他の場合には、bilinearは、つぎのメッセージを表示します。
Numerator cannot be higher order than denominator.
bilinearに線形システムの零点-極-ゲイン型と伝達関数型を区別させるには、最初の2 displaysつの入力引数が同じ向きのベクトルでなければなりません。他の場合には、bilinearは、つぎのメッセージを表示します。
First two arguments must have the same orientation.
参考
|
アナログ/ディジタルフィルタ変換のインパルス不変応答法 |
|
ローパスフィルタからバンドパスアナログフィルタへの変換 |
|
ローパスフィルタからバンドストップアナログフィルタへの変換 |
|
ローパスフィルタからハイパスアナログフィルタへの変換 |
|
ローパスフィルタからローパスアナログフィルタへの変換 |
参考文献
[1] Parks, T.W., and C.S. Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987. Pgs. 209-213.
[2] Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1989. Pgs. 415-430.
 | besself | blackman |  |