| Signal Processing Toolbox | |
Kaiserウインドウを使ったFIRフィルタ設計のパラメータを計算
Syntax
[n,Wn,beta,ftype]=kaiserord(f,a,dev) [n,Wn,beta,ftype]=kaiserord(f,a,dev,fs) c=kaiserord(f,a,dev,fs,'cell')
詳細
kaiserordは、関数fir1で使うKaiserウインドウのパラメータ、フィルタ次数nとbetaパラメータを出力します。周波数領域で仕様を設定した場合、kaiserordは、仕様を近似的に満足する最小のFIRフィルタの次数を計算します。kaiserordは、与えられたフィルタ仕様を通過帯域リップル、遮断帯域リップルに、カットオフ周波数をウインドウを利用して設計するFIRフィルタ設計に必要な型に変換します。
[n,Wn,beta,ftype] は、入力した仕様 = kaiserord(f,a,dev)
f, a, devを満足する次数n、正規化した周波数帯域のエッジ周波数Wn、重みを計算します。fは、帯域エッジを表すベクトル、aは、fで設定する帯域での希望する振幅を設定するベクトルです。fの長さは、aの長さの2倍から2を引いたものです。fとaは、共に、希望する区分的な応答関数を定義するために使います。devは、aと同じ大きさのベクトルで、各帯域毎に、出力フィルタの周波数応答と希望する振幅との差の許容範囲を設定するものです。devは、通過帯域のリップルと遮断帯域での減衰を設定します。devの要素は正の数で、フィルタのゲインの絶対値を dB で表します。
注意
Kaiserウインドウ法は、通過帯域全体で同じリップル高をもち、また、遮断帯域全体で同じリップル高をもつように制約されているので、複数の通過帯域(または、遮断帯域)をもつフィルタに対して、各帯域でのリップルを等しくしない場合、最小の通過帯域(遮断帯域)の仕様を、ベクトルdevに設定してください。
|
fir1は、得られる次数n、周波数ベクトルWn、複数帯域のゲインタイプftype、およびKaiserウィンドウパラメータbetaを使用することができます。文字列ftypeは、fir1を使うことを目的としており、ハイパスフィルタの場合'high'、バンドストップフィルタの場合は'stop'とします。複数帯域フィルタの場合、最初の帯域が遮断帯域(f = 0で始まる)の場合'dc-0'、最初の帯域が通過帯域の場合'dc-1'と設定します。
関数kaiserのパラメータf、a、およびdevによって与えられる仕様を近似的に満たすフィルタbを設計するには、つぎのようにします。
b = fir1(n,Wn,kaiser(n+1,beta),ftype,'noscale')
[n,Wn,beta,ftype] は、サンプリング周波数 = kaiserord(f,a,dev,fs)
fsを設定します。設定しない場合、または、空の場合、fsは1 HzのNyquist周波数を意味する2 Hzにデフォルト値に設定されます。したがって、特定のアプリケーションのサンプリング周波数に換算した帯域エッジを設定することができます。
c は、その要素が = kaiserord(f,a,dev,fs,'cell')
fir1へのパラメータであるセル配列です。
アルゴリズム
kaiserordは、微分器やHilbert変換器同様に、ローパスフィルタの次数推定に関する経験的に導かれた公式を使用します。複数帯域フィルタ(バンドパスフィルタなどの)に関する推定は、ローパス設計公式から導かれます。
KaiserウィンドウやそのFIRフィルタ設計への応用の基礎となる設計公式は、つぎのとおりです。
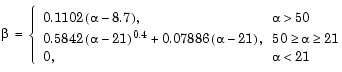
ここで、
= -20log10
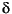は、 dB 単位で表した遮断帯域の減衰です( 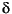p = 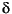sが必要であることを思い出してください)。設計公式は、つぎのように表されます。
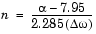
例題
0から1 kHzの通過帯域と1500 Hzから4 kHzの遮断帯域をもつローパスフィルタを設計します。5 %の通過帯域リップルと40 dBの遮断帯域減衰を設定します。
fsamp=8000; fcuts=[1000 1500]; mags=[1 0]; devs=[0.05 0.01]; [n,Wn,beta,ftype]=kaiserord(fcuts,mags,devs,fsamp); hh=fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale'); freqz(hh)
奇数長のバンドパスフィルタを設計します(ここでの奇数長は、偶数の次数を意味するため、fir1 への入力は偶数の整数でなければならないことに注意してください)。
fsamp=8000; fcuts=[1000 1300 2210 2410]; mags=[0 1 0]; devs=[0.01 0.05 0.01]; [n,Wn,beta,ftype]=kaiserord(fcuts,mags,devs,fsamp); n=n + rem(n,2); hh=fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale'); [H,f]=freqz(hh,1,1024,fsamp); plot(f,abs(H)), grid on
1500 Hzの通過帯域カットオフ、2000 Hzの遮断帯域カットオフ、0.01の通過帯域リップル、0.1の遮断帯域リップル、および8000 Hzのサンプリング周波数をもつローパスフィルタを設計します。
[n,Wn,beta,ftype]=kaiserord([1500 2000],[1 0],[0.01 0.1],8000); b=fir1(n,Wn,ftype,kaiser(n+1,beta),'noscale');
c=kaiserord([1500 2000],[1 0],[0.01 0.1],8000,'cell'); b=fir1(c{:});
注意
フィルタの長さの意味とフィルタの次数の意味を区別するよう注意してください。フィルタの長さとは、FIRフィルタ内のインパルス応答のサンプル数です。一般に、インパルス応答はn = 0から n = L-1 で順序付けられ、Lはフィルタの長さです。フィルタの次数とは、フィルタのz 変換表現の中で最も高い次数です。FIR伝達関数では、この表現は z での多項式となります。ここで、最も高いベキ乗数はzL-1 であり、最も低いベキ乗数はz0です。フィルタの次数は長さより1低い値(L-1)であり、また、z多項式のゼロの数と等しくなります。
参考
|
ウィンドウベースの有限インパルス応答フィルタの設計 − 標準応答 |
|
Kaiserウィンドウ |
|
Parks-McClellan最適FIRフィルタの次数推定 |
参考文献
[1] Kaiser, J.F., "Nonrecursive Digital Filter Design Using the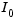 
- sinh Window Function," Proc. 1974 IEEE Symp. Circuits and Systems, (April 1974), pp. 20-23.
[2] Selected Papers in Digital Signal Processing II, IEEE Press, New York, 1975, pp. 123-126.
[3] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, pp. 458-562.
| | kaiser | lar2rc | |
は、遷移帯の最小の幅です。
