

| Signal Processing Toolbox |   |
表示
[b,a]=besself(n,Wn) [b,a]=besself(n,Wn,'ftype') [z,p,k]=besself(...) [A,B,C,D]=besself(...)
詳細
besselfは、ローパス、バンドパス、ハイパス、およびバンドストップアナログBesselフィルタを設計します。アナログBesselフィルタには、通過帯域全体に渡り、ほとんど一定の群遅延をもつという特徴があるため、通過帯域において、フィルタ処理された信号の波形が保持されます。ディジタルBesselフィルタには、この特性がないため、besselfは、ディジタルBesselフィルタの設計はサポートしていません。
[b,a] = besself(n,Wn)
は、カットオフ周波数Wnをもつn 次のローパスアナログフィルタを設計します。これは、フィルタ係数を長さn+1の行ベクトルbおよびaに、sの次数の降順に出力します。
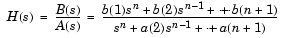
カットオフ周波数は、フィルタのゲイン応答が急激に減衰し始める周波数です。besselfの場合には、カットオフ周波数Wnは、0より大きくなければなりません。besselfで設計したBesselフィルタのゲイン応答は、カットオフ周波数で、必ずsqrt(1/2)未満となり、次数nを大きくするとより小さくなります。
Wnが2要素ベクトル Wn = [w1 w2](ここで、w1 < w2)の場合、besself(n,Wn) は、通過帯域w1 <  <
< w2をもつ2*n次のバンドパスアナログフィルタを出力します。
[b,a] = besself(n,Wn,' は、ハイパスフィルタ、または、バンドストップフィルタを設計します。ここで、ftype')
'ftype'には、つぎの文字列を設定できます。
'high':カットオフ周波数Wnをもつハイパスアナログフィルタ 'stop':Wnが2要素ベクトルWn = [w1 w2]の場合、2*n次のバンドストップアナログフィルタです。遮断帯域は、w1 <  <
< w2となります。
設定する出力引数の数により、besselfは種々の形式のアナログフィルタを実現します。零点-極-ゲイン型を得るには、つぎのように3つの出力引数を使用します。
[z,p,k] 、または、 = besself(n,Wn)
[z,p,k] = besself(n,Wn,'ftype') は、零点と極を長さn、または、2*nの列ベクトルzおよびp に、またゲインをスカラk にそれぞれ出力します。
状態空間型を得るには、つぎのように4つの出力引数を使用します。
[A,B,C,D] ここで、 = besself(n,Wn,'ftype')
A、B、C、および D は、つぎの型になります。
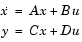
例題
10,000ラジアン/秒以上の周波数を抑制する5次アナログローパスBesselフィルタを設計し、freqsを用いてフィルタの周波数応答をプロットします。
[b,a] = besself(5,10000);
freqs(b,a) % 周波数応答をプロット
制限
ローパスBesselフィルタは、ローパスButterworthフィルタと同様に単調減少するゲイン応答をもちます。Butterworth、Chebyshev、および楕円フィルタと比較すると、Besselフィルタは、最も緩やかなロールオフをもち、減衰仕様を満たすのに最も高い次数が必要となります。
高次フィルタでは、状態空間型が数値的に最も正確であり、つぎに零点-極-ゲイン型が正確です。伝達関数係数型は最も精度が劣り、15次程度のフィルタ次数でも、数値的な問題が生じる可能性があります。
アルゴリズム
besselfは、つぎの4つのステップのアルゴリズムを実行します。
besselapを使って、ローパスアナログプロトタイプの極、零点、およびゲインを求めます。
参考
|
Besselアナログローパスフィルタのプロトタイプ |
|
Butterworthアナログおよびディジタルフィルタの設計 |
|
Chebyshev I型フィルタの設計(通過帯域リップル) |
|
Chebyshev II型フィルタの設計(遮断帯域リップル) |
|
楕円フィルタの設計 |
 | besselap | bilinear |  |