| Control System Toolbox関数リファレンス | |
零点-極-ゲインモデルを設定するか、または、LTIモデルを零点-極-ゲイン型に変換
表示
sys = zpk(z,p,k)
sys = zpk(z,p,k,Ts)
sys = zpk(M)
sys = zpk(z,p,k,ltisys)
sys = zpk(z,p,k,'Property1',Value1,...,'PropertyN',ValueN)
sys = zpk(z,p,k,Ts,'Property1',Value1,...,'PropertyN',ValueN)
sys = zpk('s')
sys = zpk('z')
zsys = zpk(sys)
zsys = zpk(sys,'inv') % 状態空間 sys のみ
詳細
zpk
零点-極-ゲインモデルの作成
sys = zpk(z,p,k)
z、極p、ゲインkの連続系零点-極-ゲインモデルを作成します。出力sysは、モデルデータを格納するZPKオブジェクトです(マニュアルの"LTIオブジェクト"を参照)。
SISOケースでは、zとpは実数または共役複素数の零点と極、kは実数値スカラのゲインです。
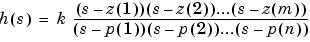
零点または極をもたないシステムの場合、zまたはpを[]に設定します。これらの2つのベクトルは同じ長さである必要はなく、モデルはプロパである必要もありません(すなわち、極の数が零点の数より少ない)。
有理数表現を使って、つぎのいずれかの方法で、ZPKモデルを作成します。
s = zpk('s')：Laplace変換sでの有理関数を使ったTFモデルを設定z = zpk('z',Ts)：離散時間変数zでの有理関数を使って、サンプル時間TsをもつTFモデルを設定一度、これらの変数を設定すると、変数s、または、zのいずれかで、実数値有理数表現として、直接、ZPKモデルを設定できます。
MIMOの零点-極-ゲインモデルを作成するためには、このモデルの各SISO要素の零点、極、ゲインを設定します。この場合、
zとpは、出力と同数の行数と入力と同数の列数をもつベクトルのセル配列であり、kは、出力と同数の行数と入力と同数の列数をもつ行列です。z{i,j}とp{i,j}は、入力jから出力iへの伝達関数の零点と極を設定します。 k(i,j)は、入力jから出力iへの伝達関数の(スカラ)ゲインを設定します。 sys = zpk(z,p,k,Ts)
は、サンプル時間Ts(秒単位)をもつ離散時間零点-極-ゲインモデルを作成します。サンプル時間を未設定のままにするには、Ts = -1、または、Ts = []と設定します。入力引数z、p、kは、連続系の場合と同様です。
sys = zpk(z,p,k,ltisys)
は、LTIモデルltisys(サンプル時間を含む)から継承した一般的なLTIプロパティをもつ零点-極-ゲインモデルを作成します。基本的なLTIプロパティの概要については、マニュアルの"基本的なプロパティ"を参照してください。
ZPKモデルの配列を作成するには、forループを使うか、zとpの多次元セル配列とkの多次元配列を使います。
上記の表示のいずれにも、つぎのプロパティ/値の組み合わせを後に続けることができます。
'PropertyName',PropertyValue
各組は、たとえば入力名やむだ時間などのモデルの固有のLTIプロパティを設定します。詳細については、setの項を参照してください。
sys = zpk(z,p,k,'Property1',Value1,...,'PropertyN',ValueN)
は、つぎのコマンドシーケンスに対するショートカットであることに注意してください。
sys = zpk(z,p,k) set(sys,'Property1',Value1,...,'PropertyN',ValueN)
sまたはzを使った有理数表現での零点-極-ゲイン型モデル
有理数表現を使って、ZPKモデルを作成することができます。これを行うため、まず、つぎのいずれかを入力してください。
s = zpk('s')：Laplace変数sで、有理関数を使って、ZPKモデルを作成z = zpk('z',Ts)：離散時間変数zでサンプリング時間Tsを使って、ZPKモデルを作成これらの変数のいずれか(s、または、z)を使って、伝達関数を有理数表現として、入力することにより、変数s、または、zで表したZPKモデルを直接設定することができます。
零点-極-ゲイン型への変換
zsys = zpk(sys)
は、任意のLTIモデルsysを零点-極-ゲイン型に変換します。出力zsysは、ZPKオブジェクトです。デフォルトでは、状態空間から零点-極-ゲインに変換する場合、zpkはzeroを使って零点を計算します。あるいは、
zsys = zpk(sys,'inv')
は、状態空間モデルに対する逆変換の公式を使って零点を計算します。このアルゴリズムは、高速ですが、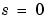
で低いゲインをもつ高次モデルに対して精度が落ちます。
変数の選択
伝達関数の場合、零点-極-ゲインモデル表示で、どの変数を使用するかを設定できます。可能な選択としては、連続系モデル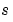
の場合 (デフォルト)
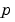、離散系モデル
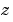の場合(デフォルト)、
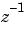、または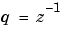
があります。デフォルトを変更する場合は、'Variable' プロパティの再設定を行います。変数を変更すると零点-極-ゲインモデルの表示のみが変化します。
例題 1
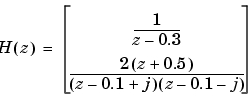
z = {[] ; -0.5}
p = {0.3 ; [0.1+i 0.1-i]}
k = [1 ; 2]
H = zpk(z,p,k,-1) % サンプル時間は未設定
例題 2
h = tf([-10 20 0],[1 7 20 28 19 5])MATLABは、つぎの出力を行います。
Transfer function:
-10 s^2 + 20 s
----------------------------------------
s^5 + 7 s^4 + 20 s^3 + 28 s^2 + 19 s + 5
zpk(h)
Zero/pole/gain:
-10 s (s-2)
----------------------
(s+1)^3 (s^2 + 4s + 5)
例題 3
つぎのように入力することで、変数zで表現された有理数表現から離散時間ZPKモデルを作成します。
z = zpk('z',0.1);
H = (z+.1)*(z+.2)/(z^2+.6*z+.09)
MATLABは、つぎの出力を行います。Zero/pole/gain: (z+0.1) (z+0.2) --------------- (z+0.3)^2 Sampling time: 0.1
アルゴリズム
zpkは、MATLAB関数rootsを使って、伝達関数に変換し、関数zeroおよびpoleを使って、状態空間モデルに変換します。
参考
frd 周波数応答データモデルに変換
get LTIモデルのプロパティを抽出
set LTIモデルのプロパティの設定
ss 状態空間モデルの設定または状態空間への変換
tf 伝達関数の設定または伝達関数への変換
zpkdata
| | zgrid | zpkdata | |