

| Control System Toolbox関数リファレンス |   |
表示
sys = tf(num,den)
sys = tf(num,den,Ts)
sys = tf(M)
sys = tf(num,den,ltisys)
sys = tf(num,den,'Property1',Value1,...,'PropertyN',ValueN)
sys = tf(num,den,Ts,'Property1',Value1,...,'PropertyN',ValueN)
sys = tf('s')
sys = tf('z')
tfsys = tf(sys)
tfsys = tf(sys,'inv') % 状態空間sysのみ
詳細
tf
は、伝達関数モデル(TFオブジェクト)を作成するため、あるいは、状態空間モデルまたは零-極-実数値モデルを伝達関数型に変換するために使用します。
伝達関数の作成
sys = tf(num,den)
は、numおよびdenで設定した分子と分母をもつ連続系伝達関数を作成します。出力sysは、伝達関数データを格納するTFオブジェクトです(マニュアルの"伝達関数モデル"を参照)。
SISOの場合、numおよびdenは、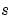 のべき乗の降順に並べられた分子と分母係数の実数値行ベクトルです。これらの2つのベクトルは、等しい長さである必要はなく、伝達関数はプロパである必要もありません。たとえば、h = tf([1 0],1) は、微分器
のべき乗の降順に並べられた分子と分母係数の実数値行ベクトルです。これらの2つのベクトルは、等しい長さである必要はなく、伝達関数はプロパである必要もありません。たとえば、h = tf([1 0],1) は、微分器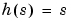 を設定します。
を設定します。
MIMO伝達関数を作成するには、SISO要素毎の分子と分母を設定します。この場合、
numとdenは、出力と同数の行数と入力と同数の列数をもつ行ベクトルのセル配列です。 num{i,j}とden{i,j}は、入力j から出力iへの伝達関数(SISO 記法による)の分子と分母を設定します。MIMO伝達関数のすべてのSISO要素が同じ分母をもつ場合、denに共通分母の行ベクトル表現を設定することができます。詳細については、つぎの例題を参照してください。
sys = tf(num,den,Ts)
は、サンプル時間Ts(秒単位)の離散時間伝達関数を作成します。サンプル時間を未設定のままにするには、Ts = -1またはTs = []と設定します。入力引数numおよびden は、連続系の場合と同様で、分子、分母係数を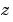 のべき乗の降順に表示しなければなりません。
のべき乗の降順に表示しなければなりません。
sys = tf(M)
は、静的ゲイン M(スカラまたは行列)を作成します。
sys = tf(num,den,ltisys)
は、LTIモデルltisys(サンプル時間を含め)から継承した一般的なLTIプロパティをもつ伝達関数を作成します。一般的なLTIプロパティの概要については、マニュアルの"基本的なプロパティ"を参照してください。
伝達関数のLTI配列の作成には、いくつかの方法があります。SISO TFモデルまたはMIMO TFモデルの配列を作成するには、多次元セル配列を使って、各SISOに関する分子と分母を設定するか、または、配列内の各TFモデルをforループを使って連続的に割り与える方法があります。詳細は、マニュアルの"LTI配列の作成"を参照してください。
上記の構文のいずれにも、つぎのプロパティ/値の組み合わせを後に続けることができます。
'Property',Value
各組は、たとえば入力名や伝達関数変数などのモデルの特定のLTIプロパティを設定します。詳細については、setの項および、つぎの例題を参照してください。
sys = tf(num,den,'Property1',Value1,...,'PropertyN',ValueN)
sys = tf(num,den) set(sys,'Property1',Value1,...,'PropertyN',ValueN)をまとめたものです。
SまたはZの有理数で表わした伝達関数
実数有理数表現を使って、TFモデルを作成することができます。まず、つぎのどちらかを行います。
s = tf('s'):Laplace変換sでの有理関数を使ったTFモデルを設定z = tf('z',Ts):離散時間変数zでの有理関数を使って、サンプル時間TsをもつTFモデルを設定これらの変数の内、一つを設定すると、sまたはzで表わした有理数表現として、伝達関数を入力することにより、変数sまたはzで表わした有理数表現として、直接TFモデルを設定することができます。
伝達関数への変換
tfsys = tf(sys)
は、任意のSSまたはZPKのLTIモデルsysを伝達関数型に変換します。出力tfsys(TF オブジェクト)は、sysの伝達関数です。デフォルトでは、状態空間モデルを伝達関数型に変換する場合、tfはzeroを使って分子を計算します。または、
tfsys = tf(sys,'inv')
は、状態空間モデルに対する逆変換式を使って分子を導きます。このアルゴリズムは高速ですが、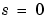 で低いゲインをもつ高次モデルに対して精度が落ちます。
で低いゲインをもつ高次モデルに対して精度が落ちます。
例題 1
入力として、current 、出力として torqueとang velocityをもつ2出力、1入力の伝達関数
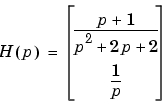
num = {[1 1] ; 1}
den = {[1 2 2] ; [1 0]}
H = tf(num,den,'inputn','current',...
'outputn',{'torque' 'ang. velocity'},...
'variable','p')
MATLABは、つぎの出力を行います。
Transfer function from input "current" to output...
p + 1
torque: -------------
p^2 + 2 p + 2
1
ang. velocity: -
p
'variable'プロパティを'p'に設定すると、結果がどのように変数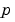 の伝達関数として表示されるかに注意してください。
の伝達関数として表示されるかに注意してください。
例題 2
s = tf('s');
H = s/(s^2 + 2*s +10);
例題 3
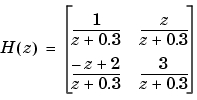
ここで、分母は、共通で、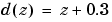 で表わし、サンプル時間は0.2秒とします。
で表わし、サンプル時間は0.2秒とします。
nums = {1 [1 0];[-1 2] 3}
Ts = 0.2
H = tf(nums,[1 0.3],Ts) % 注:共通分母d(z)に対する行ベクトル
例題 4
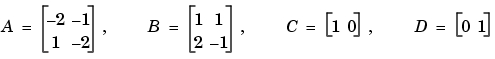
sys = ss([-2 -1;1 -2],[1 1;2 -1],[1 0],[0 1])
tf(sys)
Transfer function from input 1 to output:
s
-------------
s^2 + 4 s + 5
Transfer function from input 2 to output:
s^2 + 5 s + 8
-------------
s^2 + 4 s + 5
SISO TFモデルの10行1列の配列をforループとして使用します。
s = tf('s')
H = tf(zeros(1,1,10));
for k=1:10,
H(:,:,k) = k/(s^2+s+k);
end
この最初のステートメントは、TF配列の前に配置され、ゼロの伝達関数に合わされます。
離散時間変換
制御およびデジタル信号処理(DSP)の世界では、異なる記法を使って離散系伝達関数を設定する傾向があります。ほとんどのエンジニアは、変数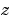 を使用して 、
を使用して 、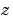 のべき乗の降順に分子、分母の項を並べます。たとえば、つぎのとおりです。
のべき乗の降順に分子、分母の項を並べます。たとえば、つぎのとおりです。
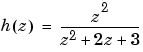
この場合、多項式 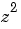 および
および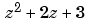 は、行ベクトル
は、行ベクトル[1 0 0] および[1 2 3]によって、それぞれ設定されます。これに対して、DSPエンジニアは、この伝達関数を
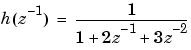
のように表し、その分子を1と設定し([1 0 0]の代わりに)、その分母を[1 2 3]と設定するほうを好みます。
これら2つの記法は、分子と分母が異なる長さをもっている場合、問題を生じます。2つの表現法での整合性を保ため、tfは選択した変数に基づいて記法を切り替えます('Variable' プロパティの値)。
| 変数 |
変換 |
'z' (デフォルト) |
行ベクトル[ak ... a1 a0]を使って多項式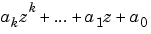 ( (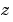 べき乗の降順に並べられた係数を設定する)。 べき乗の降順に並べられた係数を設定する)。 |
'z^-1', 'q' |
行ベクトル[b0 b1 ... bk]を使って多項式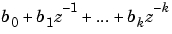 ( (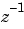 または または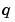 のべき乗の昇順に並べられた係数を設定する)。 のべき乗の昇順に並べられた係数を設定する)。 |
g = tf([1 1],[1 2 3],0.1)
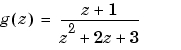
h = tf([1 1],[1 2 3],0.1,'variable','z^-1')
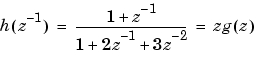
を作成します。また、DSP記法を用いる離散系伝達関数の直接設定については、filtも参照してください。
tfは、分子と分母の長さが等しくなるように、変数に独立に表現することに注意してください。特に、tfはg(分子には左側にゼロが入ります)に対して値
num = [0 1 1]; den = [1 2 3]
num = [1 1 0]; den = [1 2 3]
アルゴリズム
tfは、MATLAB関数polyを使って、零点-極-ゲインモデルに変換し、関数zeroおよびpoleを使って状態空間モデルに変換します。
参考
filt
frd 周波数応答データモデルの設定
get LTIモデルのプロパティを抽出
set LTIモデルのプロパティの設定
ss 状態空間モデルの設定または状態空間モデルへの変換
tfdata
zpk 零点-極-ゲインモデルの設定または零点-極-ゲインモデルへの変換
 | step | tfdata |  |