balreal (Control System Toolbox関数リファレンス)

状態空間実現の入力/出力の平衡化

表示

sysb = balreal(sys)
[sysb,g,T,Ti] = balreal(sys)

詳細

sysb = balreal(sys) は、LTIモデルsysに対して、等価な対角化可制御性グラミアンおよび可観測性グラミアンをもつ平衡化実現sysbを作成します(グラミアンの定義については、gramを参照)。balrealは、連続系、離散系いずれも取り扱います。sysが状態空間モデルでない場合は、まず、ssを使って自動的に状態空間型に変換されます。

[sysb,g,T,Ti] = balreal(sys) は、平衡化されたグラミアンの対角部を含むベクトルgを出力し、sysをsysbに変換するために使用する状態相似変換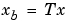および逆変換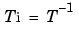も出力します。

システムが適切に正規化される場合、結合グラミアンの対角部gを使って、モデルの低次元化を行なうこともできます。gは、平衡化されたモデルの個々の状態の可制御性および可観測性のいずれも反映しているので、小さなg(i)に関連した状態を削除できます。従って、残ったものは、オリジナルシステムの重要な入/出力特性を含んだものになります。状態の削除にはmodredを使用します。

例題

つぎの零点-極-ゲインモデルを考えます。

sys = zpk([-10 -20.01],[-5 -9.9 -20.1],1)
 
Zero/pole/gain:
   (s+10) (s+20.01)
----------------------
(s+5) (s+9.9) (s+20.1)

平衡化されたグラミアンをもつ状態空間実現は、つぎのステートメントで求められます。

[sysb,g] = balreal(sys)

結合グラミアンの対角部は、つぎのようになります。

g'
 
ans =
   1.0062e-01   6.8039e-05   1.0055e-05

これは、sysbの最後の2つの状態が入力と出力にあまり関連がないことを意味しています。この場合には、

sysr = modred(sysb,[2 3],'del')

を使って、これらの状態を削除し、オリジナルのシステムを、つぎの1次近似として求めることができます。

zpk(sysr)

Zero/pole/gain:
 1.0001
--------
(s+4.97)

オリジナルのモデルと低次元化したモデルのBode応答を比較します。

bode(sys,'-',sysr,'x')

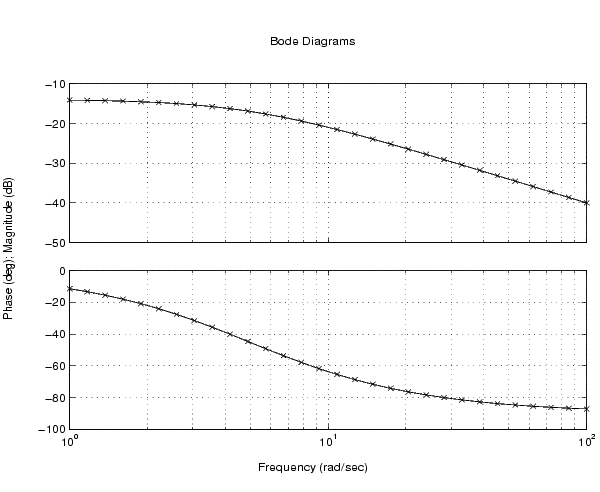
アルゴリズム

可制御性グラミアン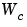および可観測性グラミアン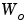をもつ、つぎのモデルを考えます。

状態座標変換は、つぎの等価モデル

を作成し、グラミアンを

に変換します。

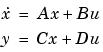
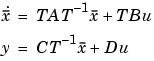
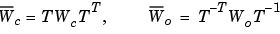
関数balrealは、つぎのような特定な相似変換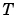

を計算します。

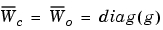
アルゴリズムの詳細については、参考文献[1,2]を参照してください。

制限

LTIモデルsysは、安定していなければなりません。さらに、状態空間モデルは可制御性と可観測性であることが必要です。

参考
gram 可制御性グラミアンと可観測性グラミアン

minreal 最小実現

modred モデルの低次元化

参考文献

[1] Laub, A.J., M.T. Heath, C.C. Paige, and R.C. Ward, "Computation of System Balancing Transformations and Other Applications of Simultaneous Diagonalization Algorithms," IEEE Trans. Automatic Control, AC-32 (1987), pp. 115-122.

[2] Moore, B., "Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduction," IEEE Transactions on Automatic Control, AC-26 (1981), pp. 17-31.

[3] Laub, A.J., "Computation of Balancing Transformations," Proc. ACC, San Francisco, Vol.1, paper FA8-E, 1980.

augstate bode