

| Mathematics |   |
境界値問題ソルバ
bvp4cMATLAB Help ブラウザを使って、MATLAB関数に対するシンタックスに関する情報を得ることができます。
BVP ソルバ
関数bvp4c は、常微分方程式(ODEs)に関する2点境界値問題を解きます。つぎの型をした1階の常微分方程式、
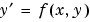
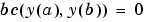
の基で、シミュレーションします。これは、つぎの型をした問題に対して、未知パラメータを含ませることができます。
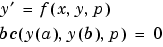
この場合、境界条件の数は、解と未知パラメータを決定するのに十分になります。
bvp4c は、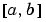 の区間で、解が連続で、また、一階微分も連続なものになります。関数
の区間で、解が連続で、また、一階微分も連続なものになります。関数bvpvalとbvp4c の出力を使って、シミュレーション区間での指定した点で、解を計算します。
bvp4cは、3ステージ Lobatto IIIa 公式を実現する有限差分コードです。これは、選点法の方程式で、選点多項式は、シミュレーション区間で、一様な4次の精度であるC1連続解を与えます。メッシュの選択と、エラーコントロールは、連続解の残差をベースにしています。
選点法は、メッシュ点を使って、積分区間をサブ区間に分割します。ソルバは、境界条件から求まる代数方程式とサブ区間に分けた選点条件を使って、グローバルシステムを解くことにより、数値解を決定します。そして、ソルバは、各サブ区間に関して、数値解のエラーを計算します。解が、許容範囲の規範を満たさない場合、メッシュを使って、再度、処理を繰り返します。ユーザは、初期メッシュの点を与え、その点に解の初期近似を与える必要があります。
BVP ソルバの基本的なシンタックス
BVP ソルバの基本的なシンタックスは、つぎのようになります。
sol = bvp4c(odefun,bcfun,solinit)
odefun |
微分方程式を計算する関数。これは、xはスカラ、dydx と yは、列ベクトルです。
odefun は、未知のパラメータのベクトルと既知 のパラメータ変数数を受け入れることができます。 | |
bcfun |
境界条件の中での残差を計算する関数。これは、 ya と yb は、 y(a) と y(b)を表す列ベクトルです。そして、res は、境界条件を満足する中での残差の列ベクトルです。bcfun は、未知のパラメータのベクトルと既知 のパラメータ変数数を受け入れることができます。 | |
solinit |
フィールドxと y をもつ構造体 | |
|
x |
初期メッシュの順番付けられたノード。境界条件は、a = solinit.x(1)と b = solinit.x(end) になります。 |
|
y |
ノード solinit.x(i)での解に対する推定 solinit.y(:,i) をもつ解に対する初期推定 |
|
構造体は、任意の名前をもつことができ、フィールドは、x とy で名前付けられます。これは、未知パラメータに対する初期推定を与えるベクトルを含んでいます。補助関数 bvpinit を使って、solinitを作成できます。詳細は、bvpinitを参照してください。 | |
出力引数sol は、ソルバで作成される構造体です。基本的な場合、構造体は、フィールドx, y, yp をもちます。
sol.x |
bvp4cで選択されるメッシュノード |
sol.y |
sol.xのメッシュ点で、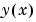 を近似 を近似 |
sol.yp |
sol.xのメッシュ点で、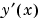 を近似 を近似 |
sol.parameters |
存在すると、ソルバで検出される未知パラメータ値 |
関数 bvpval は、出力構造体sol を使って、
[a,b]の任意の点で、数値解を計算します。
付加的なBVP ソルバ引数
よりアドバンストなアプリケーション用に、入力引数として、ソルバオプションと付加的な既知パラメータを指定できます。
|
デフォルトの積分プロパティを変更するオプションパラメータの構造体。これは、4番目の入力引数になります。sol = bvp4c(odefun,bcfun,solinit,options)BVP オプション構造体の作成と取り扱い では、ユーザが設定できる構造体の作成法やプロパティの記述法を説明しています。 |
p1,p2... |
既知 のパラメータで、ソルバは、odefun や bcfunに渡します。sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...)ソルバは、 options引数の後に、任意の数だけ設定した入力パラメータを、コールする度に、odefun や bcfunに、渡します。optionsが設定されていない場合は、options = []を使います。odefun引数リストの中で、既知のパラメータは、x, y に、存在するならば、未知のパラメータ(parameters)に続きます。dydx = odefun(x,y,p1,p2,...) dydx = odefun(x,y,parameters,p1,p2,...) bcfun 引数リストの中で、既知のパラメータは、ya、 yb、また、存在するならば、未知パラメータベクトルに続きます。res = bcfun(ya,yb,p1,p2,...) res = bcfun(ya,yb,parameters,p1,p2,...)例題は、例題:難しい BVPを解くために連続を使用を参照してください。 |
 | 境界値 ODE 問題の紹介 | BVP 問題の表現 |  |