

| Mathematics |   |
良い初期推定の作成法
境界値問題を解くために、解に対する初期推定を与える必要があります。ユーザの設定する推定の質が、ソルバの性能に影響を与え、問題全体を解くこともできます。しかし、うまい推定に達することは、境界値問題を解くために必要な事柄の大部分を占めることになります。確かに、ユーザは、問題の物理的な根源の知識を適用する必要があります。
良い推定を行う一つの方法は、比較的簡単な問題、すなわち、連続として、問題を解くことです。問題の解は、つぎの問題を解くために良い推定を与えることになります。
つぎの例題は、連続を使って、難しい問題をどのように解くかを示しています。
注意
デモ shockbvp は、つぎの例題のすべてのコードを示しています。デモは、サブ関数を使い、一つのM-ファイルの中にすべての必要な関数を配置しています。この例題を実行するためには、コマンドラインで、shockbvpと入力してください。詳細は、BVP ソルバの基本的なシンタックス と BVP 問題の表現 を参照してください。
|
例題:連続性を使って、難しい BVP を解く
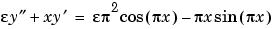
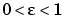 に対して、解は、
に対して、解は、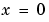 で転移層をもっています。
で転移層をもっています。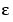 の小さな値に対して、解の中の急激な変化のために、問題は、数値的に解くことが困難になります。
の小さな値に対して、解の中の急激な変化のために、問題は、数値的に解くことが困難になります。
| 注意 この問題は、[1]に記述され、うまく作成したBVP コード COLSYS のメッシュ選択機能を示すものです。 |
1 ODE と境界条件関数のコード化
bvp4c が使用できる関数として、微分方程式と境界条件をコード化します。付加的な既知パラメータ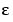 が存在するので、関数は、つぎのような型になる必要があります。
が存在するので、関数は、つぎのような型になる必要があります。
dydx = odefun(x,y,p1) res = bcfun(ya,yb,p1)
MATLAB関数shockODE と shockBCに、微分方程式と境界条件を、それぞれ、コード化しています。付加的なパラメータ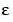 を、
を、eで表します。
function dydx = shockODE(x,y,e)
pix = pi*x;
dydx = [ y(2)
-x/e*y(2) - pi^2*cos(pix) - pix/e*sin(pix) ];
function res = shockBC(ya,yb,e)
res = [ ya(1)+2
yb(1) ];
sol = bvp4c(@shockODE,@shockBC,sol,options,e);
その後、bvp4c は、これらを計算するときに、この引数を関数shockODE と shockBC に渡します。詳細は、付加的な BVP ソルバ引数 を参照してください。
2 解析的な偏微分係数を与える この問題に対して、ソルバは、解析的な偏微分係数を利用します。つぎのコードは、関数shockJac と shockBCJacに、微係数を表しています。
function jac = shockJac(x,y,e)
jac = [ 0 1
0 -x/e ];
function [dBCdya,dBCdyb] = shockBCJac(ya,yb,e)
dBCdya = [ 1 0
0 0 ];
dBCdyb = [ 0 0
1 0 ];
bvp4cは、付加的な引数をユーザが与えるすべての関数に渡すので、shockJac と shockBCJacは、付加的な引数eを受け入れなければなりません。
オプションのFJacobian と BCJacobianを設定することで、偏微分係数を計算するために、これらの関数を使うことをbvp4c に知らせます。
options = bvpset('FJacobian',@shockJac,...
'BCJacobian',@shockBCJac);
3 初期推定の作成 初期メッシュとメッシュ点での解の値に対する推定を含む推定構造体を、bvp4c に与える必要があります。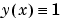 と
と 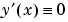 の定数推定と[-1 1]上を5等分に分割した点からなるメッシュを使って、
の定数推定と[-1 1]上を5等分に分割した点からなるメッシュを使って、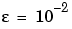 に対する問題を解きます。
に対する問題を解きます。bvpinitを使って、推定構造体を作成します。
sol = bvpinit([-1 -0.5 0 0.5 1],[1 0]);
4 連続性を使って、問題を解きます。 パラメータ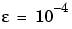 を使って、解を得るために、この例題では、
を使って、解を得るために、この例題では、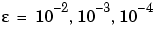 をパラメータとして、一連の問題を作成し、それを連続的(その結果を利用して)に解くことを示します。ソルバ
をパラメータとして、一連の問題を作成し、それを連続的(その結果を利用して)に解くことを示します。ソルバbvp4c は、自動的には、このような操作を行ないませんが、コード化したユーザインタフェースは、このような処理を簡単に行なえるように設計されています。bvp4c が、つぎの繰り返しの推定として、eの中の一つの値に対して作成した出力solを使います。
e = 0.1;
for i=2:4
e = e/10;
sol = bvp4c(@shockODE,@shockBC,sol,options,e);
end
plot(sol.x,sol.y(1,:))
axis([-1 1 -2.2 2.2])
title(['There is a shock at x = 0 when \epsilon ='...
sprintf('%.e',e) '.'])
xlabel('x')
ylabel('solution y')
 | BVP 問題の表現 | BVP ソルバ性能の改良 |  |