

| MATLAB Function Reference |   |
表示
sol = bvp4c(odefun,bcfun,solinit) sol = bvp4c(odefun,bcfun,solinit,options) sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...)
引数
odefun |
計算する微分方程式 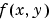 を表す引数。つぎの型をしています。 を表す引数。つぎの型をしています。dydx = odefun(x,y) dydx = odefun(x,y,p1,p2,...) dydx = odefun(x,y,parameters) dydx = odefun(x,y,parameters,p1,p2,...)ここで、 x は 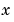 に対応するスカラで、 に対応するスカラで、y は 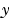 に対応する列ベクトルです。 に対応する列ベクトルです。parametersは未知パラメータで、p1,p2,... は既知パラメータです。出力 dydx は、列ベクトルです。 | |
bcfun |
境界条件 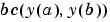 内で、残差を計算する関数です。つぎの型をしています。 内で、残差を計算する関数です。つぎの型をしています。res = bcfun(ya,yb) res = bcfun(ya,yb,p1,p2,...) res = bcfun(ya,yb,parameters) res = bcfun(ya,yb,parameters,p1,p2,...)ここで、 ya と yb は、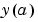 と と 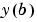 に対応したものです。 に対応したものです。parameters は、未知パラメータのベクトルで、p1,p2,... は既知パラメータです。出力 res は、列ベクトルです。 | |
solinit |
つぎのフィールドをもつ構造体 | |
|
x |
初期メッシュの順序付けられたノード。境界条件は、a = solinit.x(1)で、b = solinit(end) です。 |
|
y |
solinit.y(:,i)が、ノードsolinit.x(i)での解に対する推定である解に対する初期推定です。 |
|
parameters |
オプション。ベクトルは、未知パラメータに対する初期推定です。 |
|
構造体は、任意の名前をもてますが、フィールド名は、x, y, parametersである必要があります。補助関数bvpinitを使って、solinitを作ります。詳細は、bvpinit を参照してください。 | |
options |
オプションの積分引数。関数bvpset を使って作成する構造体。詳細は、bvpset を参照してください。 | |
p1,p2... |
オプション引数。odefun、bcfunとoptionsにユーザが指定しているすべての関数に、ソルバが渡す既知パラメータです。 | |
詳細
sol = bvp4c(odefun,bcfun,solinit)
は、つぎの型をした常微分方程式システムを積分します。
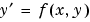
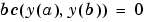
ソルバ bvp4c は、つぎの型をした問題に対して、未知パラメータ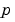 を見つけることができます。
を見つけることができます。
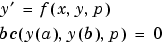
ここで、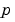 は、
は、parametersに対応します。ユーザは、solinit.parametersの中にいくつかの未知パラメータに対する初期推定をbvp4cに与えます。bvp4cソルバは、sol.parametersの中の未知パラメータの最終値を出力します。
bvp4c は、[a,b]で連続で、かつ、1階微分も連続な解を作成します。関数bvpvalとbvp4cのsolを使って、区間[a,b]で指定した点xintでの解を計算します。
yint = bvpval(sol,xint)
関数bvp4cにより戻される構造体sol は、つぎのフィールドをもっています。
x |
bvp4cで選択されたメッシュ |
y |
sol.xのメッシュで、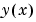 への近似 への近似 |
yp |
sol.xのメッシュ点での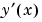 への近似 への近似 |
parameters |
必要の場合、未知パラメータ用に bvp4c で戻される値。 |
構造体 sol は、任意の名前を付けることはできますが、bvp4cは、フィールドx、y、yp、parametersを作成します。
sol = bvp4c(odefun,bcfun,solinit,options)
は、上で記述したように、デフォルトの積分プロパティをoptionsの中の値で置き換えて、解きます。このoptionsは、関数bvpsetを使って作成されます。詳細は、bvpset を参照してください。
sol = bvp4c(odefun,bcfun,solinit,options,p1,p2...)
は、定数の既知パラメータ、p1、p2、...をodefun、bcfunやoptionsにユーザ設定のすべての関数に渡します。オプションを設定しない場合は、options = []を使ってください。
例題
例題 1 境界値問題は、複数の解をもっています。そして、初期推定の目的の一つは、複数の解の中から欲しいものを指定することです。2次の微分方程式
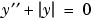
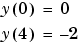
を満足する厳密な意味での2つの解をもっています。bvp4cでこの問題を解く前に、
微分方程式は、2つの1階のODEsとして表す必要があります。
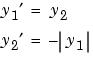
ここで、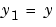 と
と 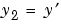 です。
このシステムは、つぎの型を必要としています。
です。
このシステムは、つぎの型を必要としています。
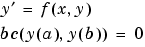
関数 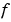 と境界条件
と境界条件 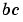 は、関数
は、関数twoode と twobcとして、MATLABにコード化されます。
function dydx = twoode(x,y)
dydx = [ y(2)
-abs(y(1))];
function res = twobc(ya,yb)
res = [ ya(1)
yb(1) + 2];
[0,4]間に等間隔に分布する5点の初期メッシュと定数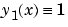 と
と 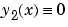 の推定から構成される推定構造体は、つぎのように作成されます。
の推定から構成される推定構造体は、つぎのように作成されます。
solinit = bvpinit(linspace(0,4,5),[1 0]);
sol = bvp4c(@twoode,@twobc,solinit);
数値解は、100点の等空間分布した点で見積もられ、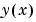 が接ぎ木のようにオプロットできます。
が接ぎ木のようにオプロットできます。
y = bvpval(sol,linspace(0,4)); plot(x,y(1,:));
solinit = bvpinit(linspace(0,4,5),[-1 0]);を使って、得られます。
例題 2
つぎの境界値問題は、未知のパラメータを含んだものです。これは、Mathieu方程式の4番目(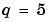 )の固有値
)の固有値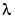 を計算するものです。
を計算するものです。
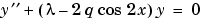
未知パラメータ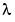 が存在するので、この2階微分方程式は、3つの境界条件により制約を受けています。
が存在するので、この2階微分方程式は、3つの境界条件により制約を受けています。
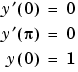
単一のM-ファイルの中で、bvp4cにより必要とされるすべての関数をサブ関数を使って、置き換えることが便利です。
function mat4bvp
lambda = 15;
solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda);
sol = bvp4c(@mat4ode,@mat4bc,solinit);
fprintf('The fourth eigenvalue is approximately %7.3f.\n',...
sol.parameters)
xint = linspace(0,pi);
Sxint = bvpval(sol,xint);
plot(xint,Sxint(1,:))
axis([0 pi -1 1.1])
title('Eigenfunction of Mathieu''s equation.')
xlabel('x')
ylabel('solution y')
% ------------------------------------------------------------
function dydx = mat4ode(x,y,lambda)
q = 5;
dydx = [ y(2)
-(lambda - 2*q*cos(2*x))*y(1) ];
% ------------------------------------------------------------
function res = mat4bc(ya,yb,lambda)
res = [ ya(2)
yb(2)
ya(1)-1 ];
% ------------------------------------------------------------
function yinit = mat4init(x)
yinit = [ cos(4*x)
-4*sin(4*x) ];
(1階のシステムに変換された)微分方程式と境界条件が、サブ関数mat4ode と mat4bcとしてコード化されます。未知パラメータが存在するために、これらの関数は、3つの入力引数を受け入れます。但し、これらの中でいくつかは、使われない可能性があります。
推定構造体 solinit は、bvpinitを使って作られます。解に対する初期推定は、関数mat4initの型の中に用意されています。正しい挙動(符号の変化する回数)をもつ境界条件を満足するので、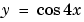 を選択しています。
を選択しています。bvpinitにコールする中で、3番目の引数(lambda = 15)は、未知パラメータ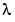 に対する初期推定を与えます。
に対する初期推定を与えます。
問題をbvp4cを使って解いた後、フィールドsol.parameters は、値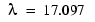 を出力し、この固有値に関連した固有韓数をプロットします。
を出力し、この固有値に関連した固有韓数をプロットします。
アルゴリズム
bvp4c は、3ステージの Lobatto IIIa公式を実現する有限差分コードです。これは、選点公式で、選点多項式は、[a,b]の中で、一様な4次の精度をもつC1連続解を与えます。メッシュの選択やエラーコントロールは、連続解の残差をベースにしています。
参考
@ (function_handle), bvpget, bvpinit, bvpset, bvpval
参考文献
Shampine, L.F., M.W. Reichelt, and J. Kierzenka, "Solving Boundary Value Problems for Ordinary Differential Equations in MATLAB with bvp4c," available at ftp://ftp.mathworks.com/pub/doc/papers/bvp/.
 | builtin | bvpget |  |