Differential Equations (Mathematics)

Mathematics

BVP 問題の表現

この節は、つぎの事柄を記述します。

MATLAB ソルバ、bvp4cを使って、境界値問題(BVPs)を解くプロセス
未知パラメータの検出
指定した点での解の計算

例題： Mathieuの方程式

この例題は、Mathieuの方程式の４番目の固有値を決定します。ここでは、２階の微分方程式を、１階の２つの微分方程式として記述する方法を示し、そして、未知のパラメータ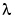をbvp4c を使って決定する方法を示します。

ここでは、まず、Mathieuの方程式の４番目(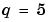)の固有値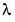を計算します。

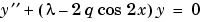
未知のパラメータ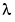が存在する場合、つぎの２階微分方程式は、３つの境界条件に従います。

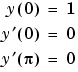
注意デモ mat4bvp は、この例題のコード全体を示すものです。デモは、サブ関数を使って、一つのM-ファイルの中に、bvp4cで必要とされるすべての関数を配置します。コマンドラインで、この例題を実行するには、mat4bvp と入力してください。詳細は、BVP ソルバの基本的なシンタックスを参照してください。

1 1次のシステムへの書き換え bvp4cを使って、方程式を、１次の微分方程式の等価なシステムとして書き換えます。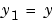と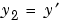を代入して、微分方程式は、2つの1次方程式として記述されます。

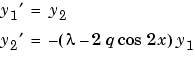
微分方程式は、未知パラメータ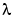に依存していることに注意してください。境界条件は、つぎのようになります。

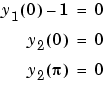
2 MATLAB で１次のODEsシステムをコード化 ユーザは、方程式を１次のシステムとして表現すると、bvp4cが使用できる関数として、それをコード化できます。未知のパラメータが存在するので、関数は、つぎの型になります。

dydx = odefun(x,y,parameters)

つぎのコードは、 "LSQR: An algorithm for sparse linear equations and sparse least squares," ACM Trans. Math. Soft., Vol.8, 1982, pp. 43-71.システムをMATLAB関数mat4odeに表したものです。

function dydx = mat4ode(x,y,lambda)
q = 5;
dydx = [   y(2)
         -(lambda - 2*q*cos(2*x))*y(1) ];

bvp4cでの未知パラメータの使用の詳細は、未知パラメータの検出を参照してください。

3 境界条件関数のコード化 ユーザは、MATLAB関数の中に境界条件をコード化する必要があります。未知パラメータが存在するので、関数は、つぎの型で表します。

res = bcfun(ya,yb,parameters)

つぎのコードは、MATLAB関数mat4bc内に表現した境界条件です。

function res = mat4bc(ya,yb,lambda)
res = [  ya(2) 
         yb(2) 
        ya(1)-1 ];

4 初期推定の作成 推定構造体 solinit は、bvpinitを使って作成されます。解と未知パラメータに対する初期推定が必要になります。

解に対する初期推定は、関数 mat4init の型で与えられます。この関数として、境界条件を満足し、正しい量的な挙動(符号の変化回数)をもっているので、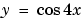を選択します。

function yinit = mat4init(x)
yinit = [  cos(4*x)
          -4*sin(4*x) ];

bvpinitへのコールの中で、3番目の引数( lambda) は、未知パラメータ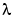として初期推定を与えます。

lambda = 15;
solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda);

この例題は、@を使って、bvpinitへの関数ハンドルとして、mat4initに渡します。

注意関数ハンドルに関する情報については、MATLABのドキュメントの中の"MATLAB を使ったプログラミング"のM-ファイルのプログラミングや、function_handle (@), func2str, str2func のリファレンスページを参照してください。

5 BVP ソルバの適用 mat4bvp例題は、関数mat4ode とmat4bc をもつ関数と共に bvp4cをコールし、構造体solinit が、bvpinit と共に作成できます。

sol = bvp4c(@mat4ode,@mat4bc,solinit);

6 結果の可視化 例題では、結果をすべて表示します。

bvp4cで求まった、未知パラメータの値を印刷します。

fprintf('The fourth eigenvalue is approximately %7.3f.\n',...
        sol.parameters)

bvpvalを使って、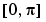の区間で、等間隔に分布している100点で数値解を計算します。そして、最初の要素をプロットします。この要素は、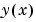の近似です。

xint = linspace(0,pi);
Sxint = bvpval(sol,xint);
plot(xint,Sxint(1,:))
axis([0 pi -1 1.1])
title('Eigenfunction of Mathieu''s equation.') 
xlabel('x')
ylabel('solution y')

bvpvalの使い方に関する情報は、特定の点での解の計算を参照してください。

つぎのプロットは、最終固有値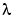 = 17.097に関連した固有韓数を示しています。

未知パラメータの検出

bvp4c ソルバは、つぎの型の問題に対して、未知パラメータ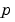を求めることができます。

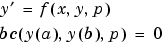
ユーザは、ベクトルsolinit.parametersの中に未知パラメータに対する初期推定をbvp4cに与えます。solinitを作成するために、bvpinit をコールすると、付加的な引数parametersの中にベクトルとして、初期推定を設定します。

solinit = bvpinit(x,v,parameters)

bvp4c 関数引数 odefun と bcfun は、各々３番目の引数として設定します。

dydx = odefun(x,y,parameters)
res = bcfun(ya,yb,parameters)

bvp4c ソルバは、各繰り返しで、未知パラメータの中間的な値を計算し、最終値をodefun や bcfunの引数parameters に渡します。ソルバは、これらの未知パラメータの最終値をsol.parametersに出力します。

指定した点の解の計算

bvp4cで実行する選点法は、積分区間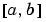全体に渡り、C¹の連続性を示します。ユーザは、bvp4cと補助関数bvpval を使って、戻される構造体sol を使って、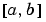の中の任意の点で近似解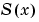を計算することができます。

Sxint = bvpval(sol,xint)

関数bvpval は、ベクトル化されています。ベクトルxintに対して、Sxintのi番目の列は、解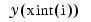を近似します。

境界値問題ソルバ良い初期推定の作成法