Mathematics

BVP ソルバ性能の改良

BVP ソルバbvp4cの中のデフォルトの積分プロパティは、一般的な問題を取り扱うことができるように選択されています。いくつかの場合、これらのデフォルト値を変更することで、ソルバの性能を改良することができます。これを行うには、Options 構造体の中の一つ、または、複数のプロパティ値を変更して、bvp4cと共に使います。

sol = bvp4c(odefun,bcfun,solinit,options)

この節では、つぎの事柄を扱います。

• Options 構造体の 作成、 変更、引用方法について
• ユーザがOptions 構造体の中で使用できるプロパティの記述

つぎのテーブル、また、それに続く、プロパティテーブルで、最も一般的に使われるプロパティカテゴリを表示し、その後に、アドバンスなものを表示します。

プロパティカテゴリ	プロパティ名
誤差の許容範囲	RelTol, AbsTol
解析的な偏微分係数	FJacobian, BCJacobian
メッシュサイズ	NMax
出力表示	Stats

注意   ソルバの効率を向上させる他の方法については、良い初期推定の作成法 とftp://ftp.mathworks.com/pub/doc/papers/bvp/で利用できるチュートリアル "bvp4c を使って、MATLAB で常微分方程式の境界値問題を解く" をチェックしてください。 available at .

BVP Options 構造体の作成と取り扱い

関数bvpset は、bvp4cに提供する options 構造体を作成します。bvpget を使って、指定したプロパティの値を、options 構造体から取得することができます。

Options 構造体の作成   関数 bvpset は、つぎのシンタックスを使って、プロパティ名/値を組として与えます。

options = bvpset('name1',value1,'name2',value2,...)

これは、名前を設定したプロパティに、値を指定したoptions構造体を作成します。指定していないプロパティは、デフォルト値が使われます。すべてのプロパティに対して、プロパティ名を判断できるユニークな名前を設定することができ、大文字、小文字の区別も行ないません。

入力引数を設定しない場合、bvpset は、すべてのプロパティ名と設定可能な値を表示し、デフォルト値を{ }で示します。

既存の options 構造体の修正   既に存在する options 構造体を修正するには、つぎのシンタックスを使います。

options = bvpset(oldopts,'name1',value1,...)

これは、oldopts の中の値を、名前/値の組を使って設定したもので書き換えます。修正した構造体は、出力引数として出力されます。同様に、つぎのコマンド

options = bvpset(oldopts,newopts)

は、構造体 oldopts と newopts を組み合わせます。出力引数 options の中で、いくつかの値は、oldopts のものをnewoptsで書き換えた結果になります。

Options 構造体の取得   関数 bvpget は、bvpsetで作成した options 構造体からプロパティ値を抽出します。

o = bvpget(options,'name')

これは、指定したプロパティ値を出力します。また、options構造体に指定したものが存在しない場合は、空行列[]を出力します。

bvpset と同様に、一意的に識別できるプロパティ名を使用することができます。

誤差許容範囲のプロパティ

bvp4cは、選点法の方程式を使うので、数値的な解は、選点方程式を満足するメッシュ点をベースにしています。メッシュ選択と誤差のコントロールは、計算した解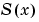 が、擾乱問題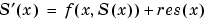の厳密解であるような解の残差をベースにしています。メッシュのサブ区間上で、解の i 番目の残差のノルム、res(i) が計算され、許容範囲より小さくすべきか、等しくすべきかを設定します。この許容範囲は、ユーザが設定できる相対許容範囲 RelTol と絶対許容範囲 AbsTolの関数になります。

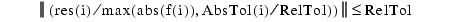
つぎのテーブルに、誤差の許容範囲のプロパティを記述します。bvpsetを使って、許容範囲を設定します。

プロパティ	値	詳細
RelTol	正のスカラ {1e-3}	残差ベクトルのすべての要素に適用する相対誤差許容範囲。のサイズに対する残差の尺度になります。デフォルト値は、10^(-3) (0.1% の精度)
AbsTol	正のスカラ、または、ベクトル {1e-6}	残差ベクトルの対応する要素に適用する絶対誤差許容範囲。AbsTol(i) は、対応する成分の値が重要でないと判断するスレッシュホールドです。スカラ値が設定されている場合、すべての要素に同一のものが適用されます。

解析的な偏微分係数

デフォルトで、bvp4c で使用するすべての偏微分係数は、有限差分で近似されます。微分方程式の解析的な偏微分係数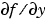と境界条件の解析的な偏微分係数 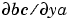と 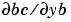を与えることで、bvp4cは、効率良くなります。問題に未知パラメータが含まれている場合、パラメータに関する偏微分係数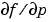 と 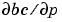も与えなければなりません。

つぎのテーブルは、解析的な偏微分プロパティを記述しています。bvpsetを使って、これらのプロパティを設定します。

プロパティ	値	詳細
FJacobian	関数	この関数は、の解析的な偏微分係数を計算します。を解く場合、dfdy = fjac(x,y)が、ヤコビアンを計算する場合、このプロパティを@fjacに設定してください。問題に未知パラメータを含む場合、[dfdy,dfdp] = fjac(x,y,p)は、偏微分係数を戻します。
BCJacobian	関数	関数は、の解析的な偏微分係数を計算します。境界条件に対して、[dbcdya,dbcdyb] = bcjac(ya,yb) は、偏微分 と を計算する場合、このプロパティを@bcjac に設定します。問題が、未知パラメータを含んでいる場合、[dbcdya,dbcdyb,dbcdp] = bcjac(ya,yb,p) は、偏微分係数も戻します。

メッシュサイズプロパティ

bvp4c は、代数方程式を解いて、メッシュの各点で、BVPの数値解を決定します。代数システムのサイズは、微分方程式の数(n) とカレントメッシュのメッシュ点数(N)に依存します。許されるメッシュ点数が非常に多い場合、計算は停止し、bvp4c は、ワーニングメッセージを表示し、その時点で求まっている解を戻します。この解は、誤差の許容範囲を満足しているものではありませんが、誤差の許容範囲を緩くするか、または、NMaxの数を増やすか、どちらかを行って、計算を再スタートするための非常に良い初期推定になります。

つぎのテーブルは、メッシュサイズプロパティを記述しています。このプロパティを設定するには、bvpset を使ってください。

プロパティ	値	詳細
正の整数	正の整数 {floor(1000/n)}	BVP を解く場合、使用可能なメッシュ点の最大数。ここで、n は、問題の中の微分方程式の数です。NMaxのデフォルト値は、代数方程式のサイズを 約1000の方程式に制限します。 2、3の微分方程式システムに対して、NMax のデフォルト値は、正確な解を得るのに十分と考えられます。

解の統計的なプロパティ

Stats プロパティは、解の統計に関する量を示します。

つぎのテーブルは、解の統計的なプロパティを記述しています。bvpset を使って、このプロパティを設定します。

プロパティ	値	詳細
Stats	on | {off}	計算に関する統計量を表示するか否かを設定。statsプロパティがonの場合、問題を解いた後で、bvp4c は、プロットします。 メッシュ内の点数 解の残差の最大値 微分方程式関数が、を計算するためにコールされる最大回数 を計算するために、境界条件関数bcfunをコールする最大回数

良い初期推定の作成法

偏微分方程式