| Mathematics | |
境界値 ODE 問題の紹介
BVP ソルバは、"LSQR: An algorithm for sparse linear equations and sparse least squares," ACM Trans. Math. Soft., Vol.8, 1982, pp. 43-71.常微分方程式を取り扱うために設計されています。
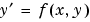
ODEsの一般的な情報については、 常微分方程式を参照してください。
境界条件を使って、興味のある解を指定
境界値問題で、対象の解は、境界条件を満足します。これらの条件は、一つの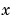
でなく複数の値で、解の値の間の関係を記述しています。bvp4cは、2点の BVP 問題を解くように設計されています。これは、区間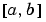
で求まった解が、つぎの境界条件を満足しなければならない問題であることを意味しています。
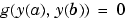
初期値問題と異なり、境界値問題は、解をもたない可能性があり、また、無限個の解をもつ可能性もあります。BVP を解くプロセスの積分部として、必要な解に対する推定を与えることが必要になります。この推定の質は、ソルバの性能にクリティカルになり、連続計算さえもそのようになります。
無限大の区間の制約をもつ問題や、特異係数を含む問題を含むBVP 問題を解くときに、他の困難が生じます。しばしば、BVP 問題は、問題を解く部分で決定されなければならない未知のパラメータ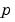
を含んでいます。
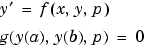
| | BVP 関数のまとめ | 境界値問題ソルバ | |
は、独立変数
は、従属変数 
は、
を表します。
の値を決定するために十分なものです。